Rozpoczął się kolejny rok szkolny, który dla dużej części uczniów oznacza ostatni rok w szkole podstawowej. Podsumowanie tego etapu edukacji będzie egzamin ósmoklasisty, pierwszy poważny sprawdzian w ich życiu, który w istotny sposób wpływać może na przyszłość – zwłaszcza na wybór szkoły ponadpodstawowej. W związku z tym warto się jak najlepiej do niego przygotować. Jeżeli również Ty stoisz przed tym wyzwaniem, rozpocznij już teraz swoje powtórki z Indeksem w Kieszeni!
Matematyka nazywana jest królową nauk. Jej dobra znajomość pozwoli Ci zrozumieć inne przedmioty ścisłe takie jak fizyka czy chemia, ale przyda się również w zagadnieniach związanych z przedsiębiorczością, wiedzą o społeczeństwie czy zagadnieniami dnia codziennego. Na koniec szkoły podstawowej powinieneś posiadać umiejętności logicznego myślenia, formułowania i rozwiązywania problemów matematycznych oraz znajomość i umiejętność stosowania niektórych ważnych twierdzeń matematycznych.
Egzamin ósmoklasisty ma na celu sprawdzenie twojej wiedzy z zakresu nauczania z całych 8 lat szkoły podstawowej. Egzamin ósmoklasisty z matematyki trwa 100 minut.
W części testowej arkusza egzaminacyjnego możesz spotkać się z zadaniami dwóch różnych typów – otwartymi i zamkniętymi.
Na egzaminie będzie do uzyskania 25 punktów:
W grupie zadań zamkniętych wyróżnia się:
Z kolei w ramach zadań otwartych czeka Cię rozwiązanie dłuższego zadania matematycznego. Przy udzielaniu odpowiedzi musisz dokonać obliczeń oraz przedstawić swoje rozumowanie. Pamiętaj! Warto czasem dodać krótki komentarz, co i dlaczego liczysz.
Skoro już wiesz, co Cię czeka, warto zastanowić się, jak się dobrze do tego przygotować. Egzamin ósmoklasisty z matematyki zbliża się z każdym dniem. Poniżej znajduje się zestaw wskazówek, których stosowanie pozwoli Ci osiągnąć jak najlepszy wynik.
Materiał, który musisz opanować do egzaminu z matematyki, jest obszerny. Często zdarza się, że uczeń niekoniecznie wie, od czego i kiedy zacząć naukę. Postaraj się zaplanować i rozłożyć swoje przygotowania na cały pozostały do egzaminu czas.
Wykorzystuj na naukę ten czas, który najbardziej jej sprzyja! Może to być wczesny poranek lub też popołudnie, z pewnością jednak nie wieczór, szczególnie jeśli za tobą bardzo intensywny dzień;
Poza nauką bieżącą związaną z codziennymi lekcjami, postaraj się wygospodarować czas na przypomnienie wcześniejszego materiału z matematyki. Może to być na przykład każdy wtorek i czwartek od 18:00 do 18:30 oraz sobota 10:00 do 11:00. Dopilnuj, aby w wyznaczonych terminach pracować nad zadaniami z matematyki.
Po zaplanowaniu materiału oraz wygospodarowaniu czasu pamiętaj, aby trzymać się tego planu! Spraw, aby czas z matematyką stał się nawykiem, ale i przyjemnością.
Dużą część wiedzy z matematyki wykorzystujemy na co dzień i to też może służyć jako ćwiczenie. Ćwiczyłeś ostatnio procenty – podczas zakupów możesz spróbować wyliczyć, czy przecena w sklepie jest poprawnie obliczona. Uczyłeś się wzorów na pole prostokąta – oblicz pole swojego pokoju (potrzebna będzie miarka – dodatkowo pole to możesz policzyć zarówno w metrach kwadratowych, jak i centymetrach kwadratowych). Jak widzisz matematyka jest wszechobecna i w każdej chwili można ją wykorzystać, a przy okazji powtórzyć ważne zagadnienia! Spróbuj to robić!
Pamiętaj, że informacje czasem uciekają z głowy! Po przerobieniu pewnego działu warto czasem do niego wrócić i zrobić z niego kilka zadań, żeby sprawdzić, czy wszystko na pewno pamiętasz.
Matematyka jest pełna wzorów. Postaraj się stworzyć własną kartę wzorów i reguł, do której będziesz mógł sięgnąć w razie problemów. Warto, aby była ona przyjazna i czytelna. Możesz w niej również wykorzystać skojarzenia i kolory!
Po ukończeniu danego działu i zrobieniu zadań możesz pochwalić się rodzicom albo pomóc koledze lub koleżance zrozumieć jakieś zadanie. Nic tak nie utrwala wiedzy, jak rozmowa o niej. Szczególnie w matematyce, w której może się zdarzyć, że dwie osoby inaczej rozwiązywały zadanie, ale obie doszły do poprawnego rozwiązania – może przy okazji też dowiesz się czegoś nowego!
Nie musisz umieć rozwiązać każdego problemu matematycznego – ba! Są na świecie problemy matematyczne, których do tej pory nie udało się nikomu rozwiązać! Jeżeli Ci coś nie wychodzi – spróbuj ponownie za jakiś czas albo spytaj kogoś o podpowiedź (nie o rozwiązanie, na początek starczy mała podpowiedź).
Pamiętaj: zdrowie jest najważniejsze! Jeżeli jesteś przemęczony lub źle się czujesz, a przyszedł czas na matematykę – pozwól sobie na odpuszczenie ten jeden raz. Uwaga: jeżeli to zrobisz, przeznacz ten czas na odpoczynek, a nie korzystanie ze smartfona czy grę na komputerze.
Zmęczony nie jesteś sobą! Pamiętaj, że spanie jest ważne. Wyspany na pewno lepiej poradzisz sobie z trudnymi zadaniami z matematyki.
Pamiętaj o ruchu! Nawet w czasie uprawiania sportów możesz zrobić albo wymyślić jakieś zadanie z matematyki. Na przykład: jeżeli pójdziesz na 3-kilometrowy spacer i zajmie Ci on 40 minut, to odpowiedz sobie na pytanie: jaka była twoja średnia prędkość?
Czas zastanowić się nad przykładowym zadaniem. Jak je rozwiązać? Na co zwrócić uwagę? Gdzie mogą być pułapki? Działów, które musisz znać, jest sporo, w związku z tym na warsztat weźmiemy jedno z zadań otwartych, gdyż to one zazwyczaj wymagają znajomości wielu zagadnień.
Zadanie pochodzi z egzaminu ósmoklasisty z 2021 roku. Od czego zacząć? Zastanów się i zaznacz na rysunku, co jest celem Twoich wyliczeń. Interesuje nas zaznaczony na czerwono odcinek DS. Teraz czas zastanowić się, co o nim wiemy oraz co dokładnie widzimy na rysunkach, a także, z jakimi wzorami to, co widzimy Nam się kojarzy.
Chwila na zastanowienie…
Kilka pierwszych wniosków:
Na rysunku mamy prostokąt ABCD. Jego pole można wyliczyć ze wzoru P = a * b
Na rysunku są również trójkąty prostokątne:
– ABC
– ACD
– ASD
– CDS
Pole trójkąta możemy wyliczyć ze wzoru P = a * h / 2, gdzie:
a – długość podstawy trójkąta,
h – wysokość opadająca na tę podstawę.
Dodatkowo w trójkątach prostokątnych można wykorzystać twierdzenie Pitagorasa,
Pamiętasz je? Zastanówmy się, czym jest szukany odcinek DS?
Tak jest – to wysokość w trójkącie ACD (wysokość pada pod kątem prostym do podstawy). Podstawą w tym przypadku jest długość AC. Dodatkowo znamy długości boków prostokąta.
Jeśli znalibyśmy pole tego trójkąta oraz długość jego podstawy moglibyśmy wyliczyć wysokość (czyli odcinek DS) ze wzoru na pole trójkąta:
P = a * h / 2
Można ją otrzymać z przytoczonego twierdzenia Pitagorasa. Wynika z niego, że:
12^(2 ) + 16^2 = |AC|^2
144 + 196 = |AC|^2
400 = |AC|^2
|AC| = √400 = 20
Można zauważyć, że przekątna AC dzieli prostokąt ABCD na dwa identyczne trójkąty. Oznacza to, że pole każdego z trójkątów – ACD oraz ACB – jest równe POŁOWIE POLA PROSTOKĄTA.
Obliczmy pole prostokąta:
P = a * b = |AB|*|AD| = 12 * 16 =192
Oznacza to, że pole trójkąta wynosi:
P_ACD= 1/2 * 192 = 96
Wykorzystujemy wzór na pole trójkąta:
P_ACD= |AC| * |SD| / 2 AC to podstawa, a SD to wysokość trójkąta ACD
96 = 20 * |SD|/ 2 *2 (mnożymy obustronnie razy 2)
192 = 20 * |SD|/2 (dzielimy obustronnie przez 20)
|SD| = 9,6
Super! Mamy odpowiedź!
Długość odcinka SD to 9,6 cm.
Rozwiązaliśmy zadanie, a przy okazji przypomnieliśmy sobie:
– wzór na pole prostokąta;
– wzór na pole trójkąta;
– Twierdzenie Pitagorasa.
Pamiętaj, każde zadanie zacznij od zastanowienia się, co jest jego celem, co wiesz o tym zadaniu oraz jakie zależności i twierdzenia mogą się przydać w rozwiązaniu!
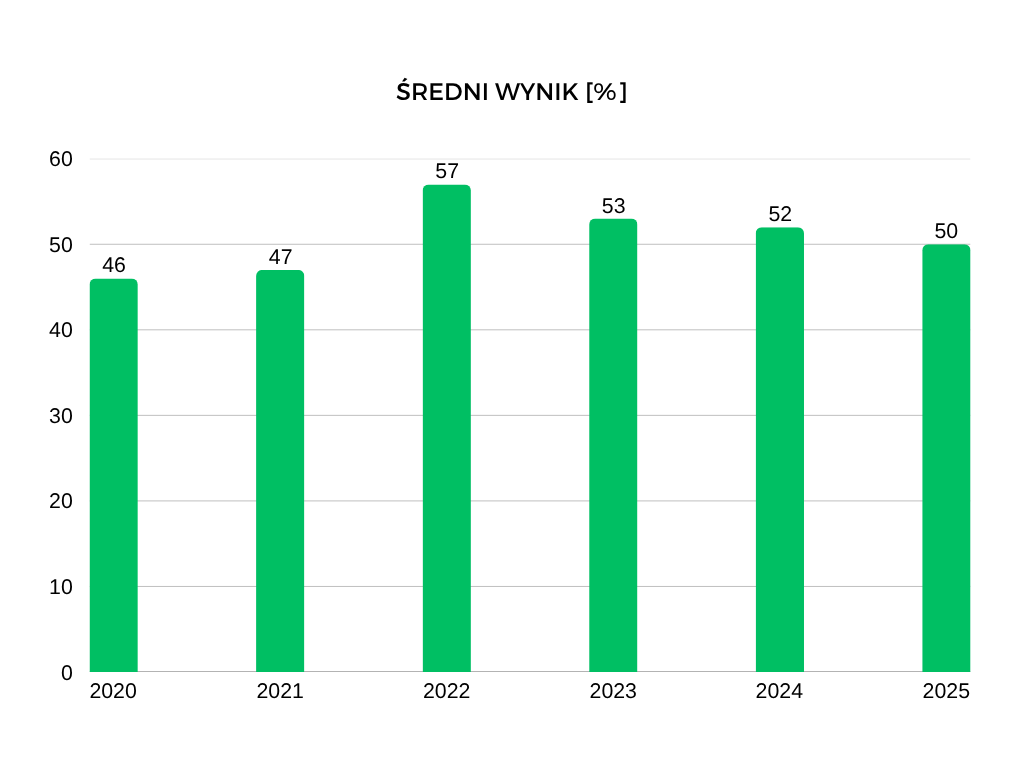
Średnie wyniki egzaminu ósmoklasisty z matematyki na przestrzeni ostatnich lat wykazują stopniowy wzrost w pierwszych latach, a następnie pewne wahania. W 2019 roku, kiedy egzamin został przywrócony, uczniowie uzyskali średnio 45%. W kolejnych latach wyniki nieznacznie rosły – 46% w 2020 roku i 47% w 2021 roku. Największy wzrost nastąpił w 2022 roku, kiedy średni wynik wyniósł aż 57%. W latach kolejnych zauważalny był spadek – 53% w 2023 roku, 52% w 2024 roku oraz 50% w 2025 roku.
Jeżeli szukasz idealnego kursu przygotowującego do egzaminu ósmoklasisty z języka polskiego zachęcamy do kontaktu! Warto nas wybrać, ponieważ w ten sposób zapewniasz sobie w pełni profesjonalne przygotowanie.
Strona przygotowana przez Zyskowni.pl
Zakładamy Ci konto na naszej platformie e-learningowej, na której znajdują się materiały, artykuły popularnonaukowe, czy nagrania video! Możesz tam bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane do sprawdzenia prace.
Na platformie otrzymujesz moduły - zestawy materiałów z prezentacjami, skryptami, testami, kartkówkami. Z nimi pracujesz w dowolnym miejscu - w domu, w podróży, w bibliotece.
Na platformie, gdzie odbywa się kurs możesz zadawać pytania 24h na dobę 7 dni w tygodniu - Prowadzący są tam po to by zawsze Ci pomóc i rozwiać Twoje wątpliwości.
Twój progres w nauce jest kontrolowany wraz z każdym kolejnym modułem - służą temu wszelkie kartkówki, testy i sprawdziany, które rozwiązane odsyłasz i otrzymujesz szczegółowy klucz.
Celujesz w świetny wynik na egzaminie ósmoklasisty? A może potrzebujesz tylko usystematyzować posiadaną wiedzę? Nieważne - nasz kurs (tempo pracy i materiały oraz pomoc Prowadzącego) jest zawsze dopasowany do aktualnego stanu Twoich umiejętności i oczekiwań.
Na platformie otrzymasz nielimitowany w okresie przygotowań dostęp do nagrań video, na których nasz zespół merytoryczny przeprowadzi Cię przez najbardziej wymagające i najczęściej pojawiające się na arkuszu zagadnienia egzaminacyjne.
Indywidualny kurs e-learningowy
egzamin ósmoklasisty
Wolisz uczyć się we własnym tempie i na własnych zasadach? W takim razie kurs e-learningowy jest stworzony właśnie dla Ciebie!
Nowoczesna forma indywidualnej nauki zdalnej (start: natychmiast lub we wskazanym terminie)
Dostęp do dedykowanej platformy do nauki e-learningowej
Harmonogram przygotowań dostosowany do dostępności ucznia
Przypisany opiekun merytoryczny prowadzący kurs
Komplet materiałów podzielonych na moduły tematyczne, a w każdym z nich: prezentacje, testy, kartkówki, skrypty, karty pracy i zadania egzaminacyjne
Materiały video – do kursu dołączone są nagrania video, na których członkowie zespołu merytorycznego IWK tłumaczą najtrudniejsze lub najbardziej prawdopodobne w wystąpieniu na egzaminie zagadnienia
Indywidualne podejście – otrzymujesz dostęp do naszej dedykowanej platformy edukacyjnej z pomocami naukowymi, na której możesz bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane prace.
Regularnie sprawdzane postępy
Ciągła możliwość kontaktu z Prowadzącym
Dzięki nowoczesnej formie nauki nasze kursy są dostępne dla uczniów z całej Polski – możesz dołączyć do nich niezależnie od miejsca zamieszkania i zacząć przygotowania już dziś! Skontaktuj się z nami i nie odkładaj decyzji na później – do egzaminu ósmoklasisty coraz bliżej!
Grupowy kurs całoroczny
egzamin ósmoklasisty
Chcesz solidnie przygotować się do egzaminu ósmoklasisty? Wolisz regularne zajęcia w grupie i stałe wsparcie prowadzącego? Jeśli tak, kurs grupowy będzie idealnym wyborem dla Ciebie!
46 godzin lekcyjnych zajęć (23 spotkania) + prace domowe
Forma stacjonarna (w salach w Warszawie) lub webinarowa (zajęcia online na żywo)
Nagrania z zajęć webinarowych oraz nagrania umożliwiające nadrobienie materiału osobom zapisującym się po rozpoczęciu kursów stacjonarnych
Możliwość wyboru grupy zajęciowej (harmonogram pojawi się w lipcu 2026 r.)
Pomoc pomiędzy zajęciami – ciągła możliwość kontaktu z Prowadzącym przez dedykowaną grupę zajęciową
Materiały z zajęć w formie cyfrowej
Regularne zajęcia pomagają utrzymać systematyczność w nauce i realnie wpływają na lepsze wyniki na egzaminie ósmoklasisty. Co roku wielu naszych uczniów z różnych części Polski osiąga wysokie rezultaty. Zapisz się na zajęcia już dziś i przygotuj się z nami do egzaminu ósmoklasisty!