W tym krótkim tekście zajmiemy się zagadnieniem fal, a w szczególności fal stojących i rezonansów. Mimo że zagadnienie wydaje się bardzo proste, to jednak jest to zagadnienie niezwykle ważne, więc nie można go zbagatelizować. W przypadku osoby przygotowującej się do Olimpiady Fizycznej to bardzo ważna kwestia, bo po prostu pojawia się relatywnie często. Z punktu widzenia początkującego fizyka jest też istotne ze względu na niezwykłą uniwersalność.
Ogólny opis fali stojącej jest niezależny od tego, czy opisujemy drgania naciągniętej struny, stojącą falę akustyczną, mod wnęki laserowej czy cząstkę kwantową w studni potencjału. Podobnie jak na zajęciach w ramach Indeksu w Kieszeni zaczniemy od rzeczy prostych, szybko jednak rozszerzając materiał poza omawiany zazwyczaj na lekcjach fizyki.
Źródło: pl.freepik.com
Na początek przypomnijmy sobie kilka podstawowych definicji i wzorów właściwych dla fali harmonicznej, czyli takiej, której wychylenie Ψ (które może być odchyłką od średniego ciśnienia, fizycznym przemieszczeniem, polem elektrycznym czy czymkolwiek innym). W danym położeniu x i czasie t wyraża się ono wzorem:
Ψ(x, t) = A sin (ωt − kx + ϕ).
We wzorze tym A oznacza oczywiście amplitudę drgań. Pochylmy się teraz nad interpretacją wielkości ω, nazywanej częstością kołową. Dla ustalonego położenia x wychylenie wraca do stanu początkowego po ωt = n 2π. Wiemy, że najkrótszy czas, po jakim układ wraca do stanu początkowego, nazywa się okresem i oznacza się go przez T. W związku z tym dla n = 1 możemy ten warunek zapisać jako ωT = 2π. Ostatecznie więc otrzymujemy:
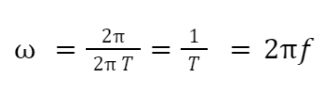
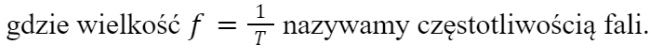
Jak zatem widać, częstość ω to nic innego jak pomnożona przez 2π częstotliwość. Najczęściej jest tak, że wielkości ω lubią używać teoretycy, natomiast wszystkie przyrządy doświadczalne posługują się zawsze częstotliwością f .
W pełni porównywalną analizę można przeprowadzić dla tak zwanej liczby falowej k. Dla ustalonego czasu t wychylenie fali harmonicznej powraca do stanu początkowego, jeśli przesuniemy się o takie ∆x, że k∆x = n 2π. Analogiem okresu tylko w przestrzeni, a nie w czasie, jest oczywiście długość fali, zazwyczaj oznaczana przez λ. Zatem powtarzając dokładnie rozumowanie dotyczące częstości, otrzymujemy, że:
Pozostaje zatem jedynie przypomnieć sobie interpretację wielkości ϕ, nazywanej fazą. Wielkość ta określa, w jakim stanie znajduje się fala dla czasu t = 0. Innymi słowy, można ją rozumieć jako analog położenia początkowego w ruchu harmonicznym.
Powróćmy jednak do wzoru pierwszego. Spróbujmy przeanalizować, jak wygląda ruch fali określony tym wzorem. W tym celu skupmy się na konkretnym miejscu fali, na przykład na którymś ze szczytów. Dla danego położenia określonego szczytu od czasu x(t) argument sinusa powinien być cały czas stały (sinus równy 1). Możemy zatem napisać:
Z czego możemy odczytać prędkość przemieszczenia się grzbietu fali jako:
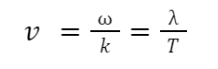
Mamy już komplet standardowych wzorów, dotyczących fali harmonicznej. Przyjrzyjmy się teraz, co się stanie, gdy nałożymy na siebie dwie fale harmoniczne, biegnące w przeciwnych kierunkach. Szczęśliwie kierunek biegu fali harmonicznej można z łatwością odwrócić. Wystarczy zamienić znak liczby falowej. Można szybko zauważyć, że prowadzi to do odwrócenia znaku prędkości. Dla wygody pominiemy przy tym fazę ϕ.
W tej sytuacji wychylenie Ψ, zgodnie z zasadą superpozycji, pozwalającej nam bezkarnie nakładać na siebie fale poprzez proste ich dodawanie do siebie, będzie wynosić:
Korzystając ze wzoru:
możemy to wyrażenie przekształcić, otrzymując:
Należy zwrócić uwagę, że w celu uniknięcia znaku minus w funkcji cos (kx) została wykorzystana parzystość tej funkcji.
Jako przykład możemy podać falę stojącą na napiętej strunie. Została ona zilustrowana na grafice nr 1. Jak widać, pewne miejsca struny, zaznaczone na czerwono, pozostają nieruchome. Nazywa się je węzłami fali stojącej. Z kolei te punkty, dla których amplituda jest największa, nazywa się strzałkami. Warunki brzegowe najczęściej wymuszają położenie węzłów na krańcach rozważanej przestrzeni. Na przykład nie może być wychylenia w miejscach zaczepu drgającej struny. Czasem jednak przez warunki brzegowe wymuszane jest położenie strzałek. Skupmy się jednak na przypadku struny, na której krańcach wychylenie musi zawsze wynosić zero. Jakie są dozwolone długości fali stojącej na takiej strunie?
Grafika 1.
Odpowiedź na to jest bardzo prosta. Na całej długości struny musi się zmieścić całkowita ilość połówek długości fali. Oznacza to, że:
Oznacza to, że tylko długości fali dane przez 2L/n są dozwolone dla napiętej, swobodnie drgającej struny. Znając prędkość rozchodzenia się fali v w strunie, możemy łatwo przeliczyć te długości fali na odpowiadające im częstotliwości. Dozwolone częstotliwości to:
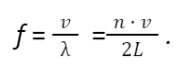
Oznacza to, że dozwolone częstotliwości są od siebie równo odległe.
Należy w tym momencie zastanowić się nad tym, co dokładnie znaczy stwierdzenie, że tylko pewne konkretne długości fali lub częstotliwości są dozwolone. Oczywiście możemy przyłożyć zawsze zewnętrzną siłę, która wymusi drgania struny z inną częstością, jednak swobodna struna będzie falować w taki sposób, że wypadkowe falowanie okaże się superpozycją drgań o dozwolonych częstościach i długościach fali.
Podobna, lecz nieco prostsza sytuacja ma miejsce w przypadku masy na sprężynce. Nieważne jak początkowo naciągniemy sprężynkę, drgania zawsze będą się odbywać z jedną, dobrze określoną częstotliwością. Tym razem system jest bardziej skomplikowany niż w przypadku struny, bo ta ostatnia może początkowo przyjąć dowolny kształt, lecz jej drganie nadal będzie odpowiadać pewnym dobrze określonym częstościom.
Okazuje się, że częstości te odpowiadają częstościom rezonansowym. Intuicyjnie jest to jasne, że częstości swobodnych drgań muszą odpowiadać rezonansom, gdyż ten warunek pozwala na akumulację energii w drganiach. W przypadku, gdy siła wymuszająca ma inną częstość niż ta cechująca drgania własne, naprzemiennie wzmacnia ona i osłabia drgania, przekazując energię systemowi w sposób nieefektywny.
Pochylmy się jeszcze raz nad istotnym faktem, że całkowity ruch napiętej struny jest superpozycją fal stojących o pewnych jasno określonych częstościach. Wyobraźmy sobie, że wychylamy napiętą, wiotką strunę w pewien początkowy kształt, po czym pozwalamy jej falować, nie nadając prędkości początkowej. Wiemy, jak ewoluuje każda z dozwolonych długości fali. Każda z nich po prostu oscyluje z odpowiednią częstością.
Spróbujmy w takim razie zapisać początkowe wychylenie Ψ w postaci:
Ψ(x) = A1 sin (k1x) + A2 sin (k2x) + A3 sin (k3x)…,
gdzie ki to kolejne dozwolone liczby falowe a Ai to odpowiadające im amplitudy. Teraz łatwo możemy policzyć, jak dalej będzie ewoluować struna. Wystarczy pomnożyć każdy sinus przez cosinus drgający z odpowiednią częstotliwością:
Ψ(x, t) = A1 sin (k1x) cos (ω1t) + A2 sin (k2x) cos (ω2t) + A3 sin (k3x) cos (ω3t)…
Zrozumienie szczegółów matematycznych dotyczących tego, jak dokonać rozłożenia Ψ(x) na sinusy o dozwolonych liczbach falowych, wymaga pewnego przygotowania, jest jednak stosunkowo proste. Ewolucję struny o pewnym arbitralnym początkowym wychyleniu, wyliczoną wyżej opisaną metodą, ilustruje grafika 2.
Grafika 2.
W tym momencie szkoda by było nie uwzględnić jeszcze jednego elementu, mianowicie tłumienia. Zazwyczaj szybciej tłumione są drgania o wyższej częstotliwości. Możemy zatem zmodyfikować wzór na ewolucję swobodnej struny w następujący sposób:
gdzie e oraz α to pewne dodatnie liczby. Czynnik e−αkit będzie malał z czasem tym szybciej, im większe ki, jest to zatem zgodne z intuicją, że najsilniej tłumione powinny być najwyższe częstości. Ewolucję struny zadaną tym wzorem ilustruje grafika 3. Jak widać, w tym przypadku drgania wyglądają już bardzo naturalnie. Nagranie w zwolnionym tempie struny gitarowej powinno wyglądać w zbliżony sposób.
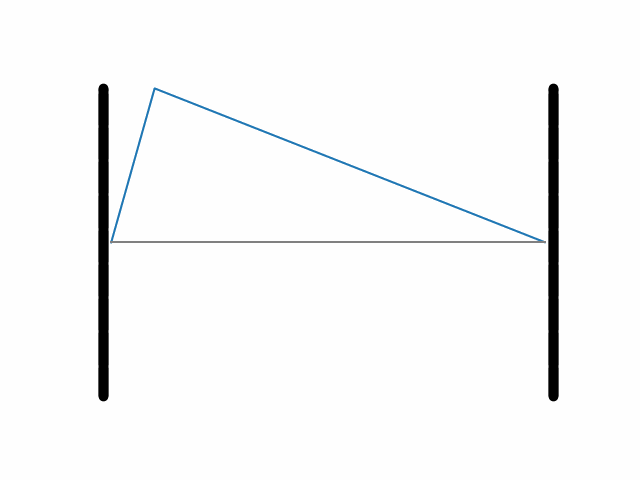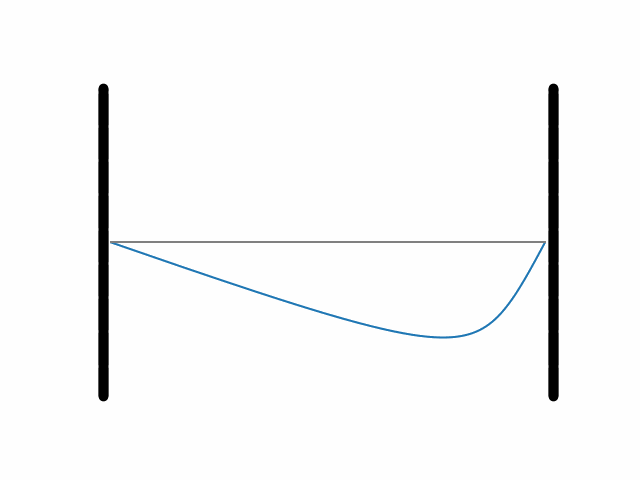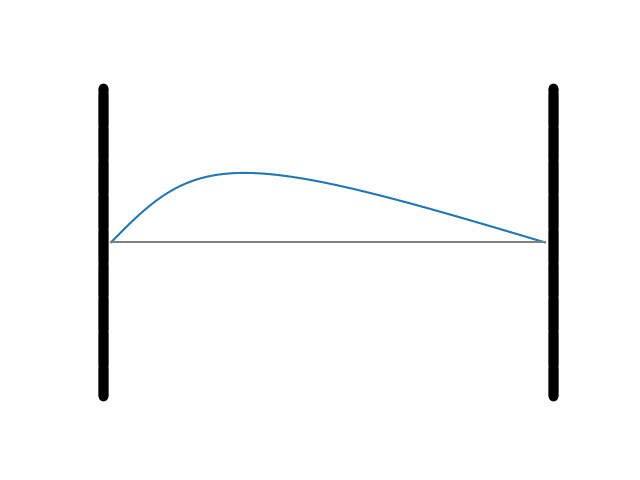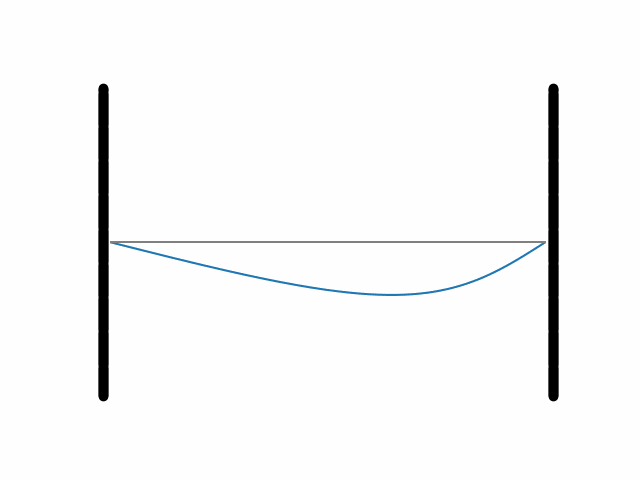
Grafika 3.
Na koniec chciałbym poczynić jedną uwagę uzupełniającą. Podczas okazji analizy fal stojących, przy pewnych określonych warunkach brzegowych, w dość nieoczekiwany sposób okazało się, że tylko drgania o pewnych określonych częstościach są dozwolone.
Czy z czymś nam się to nie kojarzy? Przecież w analogiczny sposób w mechanice kwantowej pojawiają się skwantowane poziomy energetyczne! Oczywiście z tą różnicą, że tam rolę wychylenia spełnia funkcja falowa. Niemniej stany cząstki o określonej energii to nadal nasze poczciwe fale stojące.
Strona przygotowana przez Zyskowni.pl
Zakładamy Ci konto na naszej platformie e-learningowej, na której znajdują się materiały, artykuły popularnonaukowe, czy nagrania video! Możesz tam bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane do sprawdzenia prace.
Na platformie otrzymujesz moduły - zestawy materiałów z prezentacjami, skryptami, testami, kartkówkami. Z nimi pracujesz w dowolnym miejscu - w domu, w podróży, w bibliotece.
Na platformie, gdzie odbywa się kurs możesz zadawać pytania 24h na dobę 7 dni w tygodniu - Prowadzący są tam po to by zawsze Ci pomóc i rozwiać Twoje wątpliwości.
Twój progres w nauce jest kontrolowany wraz z każdym kolejnym modułem - służą temu wszelkie kartkówki, testy i sprawdziany, które rozwiązane odsyłasz i otrzymujesz szczegółowy klucz.
Celujesz w świetny wynik na egzaminie ósmoklasisty? A może potrzebujesz tylko usystematyzować posiadaną wiedzę? Nieważne - nasz kurs (tempo pracy i materiały oraz pomoc Prowadzącego) jest zawsze dopasowany do aktualnego stanu Twoich umiejętności i oczekiwań.
Na platformie otrzymasz nielimitowany w okresie przygotowań dostęp do nagrań video, na których nasz zespół merytoryczny przeprowadzi Cię przez najbardziej wymagające i najczęściej pojawiające się na arkuszu zagadnienia egzaminacyjne.
Indywidualny kurs e-learningowy
egzamin ósmoklasisty
Wolisz uczyć się we własnym tempie i na własnych zasadach? W takim razie kurs e-learningowy jest stworzony właśnie dla Ciebie!
Nowoczesna forma indywidualnej nauki zdalnej (start: natychmiast lub we wskazanym terminie)
Dostęp do dedykowanej platformy do nauki e-learningowej
Harmonogram przygotowań dostosowany do dostępności ucznia
Przypisany opiekun merytoryczny prowadzący kurs
Komplet materiałów podzielonych na moduły tematyczne, a w każdym z nich: prezentacje, testy, kartkówki, skrypty, karty pracy i zadania egzaminacyjne
Materiały video – do kursu dołączone są nagrania video, na których członkowie zespołu merytorycznego IWK tłumaczą najtrudniejsze lub najbardziej prawdopodobne w wystąpieniu na egzaminie zagadnienia
Indywidualne podejście – otrzymujesz dostęp do naszej dedykowanej platformy edukacyjnej z pomocami naukowymi, na której możesz bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane prace.
Regularnie sprawdzane postępy
Ciągła możliwość kontaktu z Prowadzącym
Dzięki nowoczesnej formie nauki nasze kursy są dostępne dla uczniów z całej Polski – możesz dołączyć do nich niezależnie od miejsca zamieszkania i zacząć przygotowania już dziś! Skontaktuj się z nami i nie odkładaj decyzji na później – do egzaminu ósmoklasisty coraz bliżej!
Grupowy kurs całoroczny
egzamin ósmoklasisty
Chcesz solidnie przygotować się do egzaminu ósmoklasisty? Wolisz regularne zajęcia w grupie i stałe wsparcie prowadzącego? Jeśli tak, kurs grupowy będzie idealnym wyborem dla Ciebie!
46 godzin lekcyjnych zajęć (23 spotkania) + prace domowe
Forma stacjonarna (w salach w Warszawie) lub webinarowa (zajęcia online na żywo)
Nagrania z zajęć webinarowych oraz nagrania umożliwiające nadrobienie materiału osobom zapisującym się po rozpoczęciu kursów stacjonarnych
Możliwość wyboru grupy zajęciowej (harmonogram pojawi się w lipcu 2026 r.)
Pomoc pomiędzy zajęciami – ciągła możliwość kontaktu z Prowadzącym przez dedykowaną grupę zajęciową
Materiały z zajęć w formie cyfrowej
Regularne zajęcia pomagają utrzymać systematyczność w nauce i realnie wpływają na lepsze wyniki na egzaminie ósmoklasisty. Co roku wielu naszych uczniów z różnych części Polski osiąga wysokie rezultaty. Zapisz się na zajęcia już dziś i przygotuj się z nami do egzaminu ósmoklasisty!