
Jednokładność to jedno z podstawowych pojęć w geometrii, z którym uczniowie spotykają się już na wczesnym etapie nauki, a które wraca w bardziej zaawansowanej formie na egzaminach i konkursach. W matematyce opisuje ona szczególny rodzaj przekształcenia, pozwalający badać zależności między figurami podobnymi, skalą oraz położeniem punktów w przestrzeni. Zrozumienie tego zagadnienia wymaga nie tylko zapamiętania definicji, ale także umiejętności analizy i interpretacji zależności geometrycznych.
Najważniejsze informacje, których dowiesz się z tego artykułu:
Zanim przejdziemy do wzorów i rozwiązywania przykładów, warto uporządkować najważniejsze pojęcia związane z tym zagadnieniem. Dobra znajomość terminów takich jak środek, skala czy obraz punktu pozwala lepiej zrozumieć sens geometryczny całego zagadnienia i ułatwia dalszą pracę z definicją oraz własnościami.
Jednokładność to przekształcenie geometryczne, w którym każdemu punktowi przyporządkowuje się punkt leżący na półprostej wychodzącej ze środka jednokładności.
Odległość punktu obrazu od środka jest równa wartości bezwzględnej współczynnika skali pomnożonej przez odległość punktu wyjściowego. Dla współczynnika dodatniego punkty leżą na tej samej półprostej, a dla ujemnego – na przeciwnej.
Odległość punktu obrazu od środka jest wielokrotnością odległości punktu wyjściowego, a wielokrotność tę określa współczynnik skali.
Formalna definicja mówi, że jest to przeobrażenie płaszczyzny określone przez:
Jeżeli k>0 obraz punktu leży po tej samej stronie środka, a gdy k<0 po stronie przeciwnej. W tym sensie jednokładność może być także rozpatrywana jako zmianę związaną z kierunkiem i zwrotem, podobnie jak wektor.
Wzory pozwalają przejść od opisu geometrycznego do obliczeń, dzięki czemu można precyzyjnie wyznaczać długości, współrzędne punktów oraz relacje między figurami przed i po zmianie.
W przykładach rachunkowych najczęściej wykorzystuje się wzory, które opisują zależność długości odcinków przed i po zmianie. Jeśli odcinek ma długość a’, to po jednokładności jego nowa długość wynosi: a′=|k|xa.
Oznacza to, że wszystkie odcinki zmieniają się proporcjonalnie, a figury pozostają podobne.
Zagadnienie to można interpretować również jako zmianę powstałą przed złożeniem odpowiednich operacji geometrycznych, takich jak przesunięcie, skalowanie i – w przypadku ujemnej skali – symetria środkowa. Takie spojrzenie bywa szczególnie przydatne w ćwiczeniach bardziej zaawansowanych.
Źródło: www.pixabay.com
W układzie współrzędnych zagadnienie to można zapisać za pomocą prostych równań. Jeżeli środek jednokładności znajduje się w punkcie (0,0), a punkt A(x,y) przechodzi w punkt A′(x′,y′), to zachodzi zależność:
x′=kx, y′=ky
Dzięki temu łatwo obliczysz współrzędne obrazu po przeobrażeniu.
Obliczanie skali przy jednokładności polega na porównaniu długości odpowiadających sobie odcinków przed i po przekształceniu. Skala jest ilorazem tych długości:
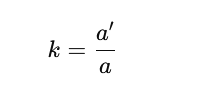
W praktyce:
Treść: dany jest odcinek o długości 4 cm. Po jednokładności jego długość wynosi 10 cm. Oblicz skalę jednokładności.
Rozwiązanie: skalę obliczamy jako iloraz długości obrazu i oryginału:
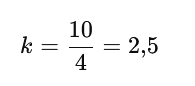
Odpowiedź: skala jednokładności wynosi k=2,5.
Treść: punkt A(2,−1), poddano jednokładności o skali k=3 względem początku układu współrzędnych. Wyznacz współrzędne punktu A′.
Rozwiązanie: w jednokładności względem punktu (0,0) współrzędne mnożymy przez skalę:
x′=3×2=6, y′=3x(−1)=−3
Odpowiedź: punkt po jednokładności ma współrzędne A′(6,−3).
Jednokładność ma kilka istotnych własności, które pomagają szybko rozwiązywać przykłady:

Źródło: www.pixabay.com
Jednokładność ma zastosowanie nie tylko w ćwiczeniach szkolnych. Występuje m.in. przy:
Dobra znajomość tego zagadnienia znacząco poszerza matematyczną wiedzę i ułatwia rozwiązywanie zadań problemowych.
Jednokładność bardzo często pojawia się w zadaniach o podwyższonym stopniu trudności, także jako element bardziej złożonych konstrukcji geometrycznych. W takim wypadku znajomość wzorów nie wystarczy – potrzebne jest głębokie rozumienie przekształceń i ich własności.
Przygotowanie do Olimpiady Matematycznej z Indeksem w Kieszeni pozwala uporządkować wiedzę z geometrii, nauczyć się pracy z przekształceniami oraz rozwiązywać zadania krok po kroku, dokładnie tak, jak wymagają tego konkursy i egzaminy. To dobre wsparcie dla uczniów, którzy chcą rozwijać swoje umiejętności ponad standardowy program szkolny.
Jednokładność to przekształcenie, które warto dobrze opanować, ponieważ łączy w sobie elementy geometrii klasycznej i analitycznej. Znajomość definicji, wzorów oraz sposobów obliczania skali pozwala sprawnie rozwiązywać zadania egzaminacyjne i lepiej rozumieć zależności między kształtami. To jedno z tych zagadnień, które po zrozumieniu staje się intuicyjne i bardzo praktyczne.
Jednokładność to przekształcenie polegające na powiększeniu lub pomniejszeniu względem jednego punktu.
Tak, dane jednokładności są zawsze podobne do wyjściowych.
Rodzaj jednokładności zależy od wartości współczynnika skali – dodatniej, ujemnej lub równej 1.
Tak, bardzo często stanowi element bardziej złożonych zadań geometrycznych.

Strona przygotowana przez Zyskowni.pl