
Każdemu uczestnikowi Olimpiady Matematycznej na pewno znany jest charakterystycznie zacieniowany kształt trójkąta. W tym wpisie Jagoda, prowadząca olimpijski kurs w Indeksie w Kieszeni, rzuci więcej światła na to niezwykle ciekawe zagadnienie. Po lekturze gorąco zachęcamy do zajrzenia na częściej naszej strony, którą poświęciliśmy przygotowaniem właśnie do Olimpiady Matematycznej, pod okiem zwycięzców i laureatów najwyższych miejsc poprzednich edycji!
Narysujmy na kartce wierzchołki trójkąta równobocznego oraz pewien losowo wybrany punkt – nazwijmy go $P_0$. Następnie losujemy jeden z wierzchołków trójkąta i wyznaczamy środek odcinka łączącego go z $P_0$ – nazwijmy go $P_1$. Dla należy wykonać tę samą procedurę, aby uzyskać punkt $P_2$ – za każdym razem od nowa losujemy wierzchołek trójkąta.
Te kroki powtarzamy wiele razy. Brzmi to bezsensownie i większość czytelników zapewne nie spodziewa się otrzymania w ten sposób czegoś ambitniejszego niż losowe, regularne skupisko kropek. Ale…
Gdy narysujemy w ten sposób kilkadziesiąt punktów, z gąszczu kropek zaczyna wyłaniać się niespodziewany kształt. Gdy (prawdopodobnie już przy użyciu komputera zamiast kartki i ołówka) narysujemy kilka tysięcy, mamy pewność. Kropki ułożyły się niemal idealnie w regularny kształt kojarzący się z wycinanką ludową, ten sam, który możemy podziwiać na każdym arkuszu z treściami zadań Olimpiady Matematycznej – w trójkąt Sierpińskiego!
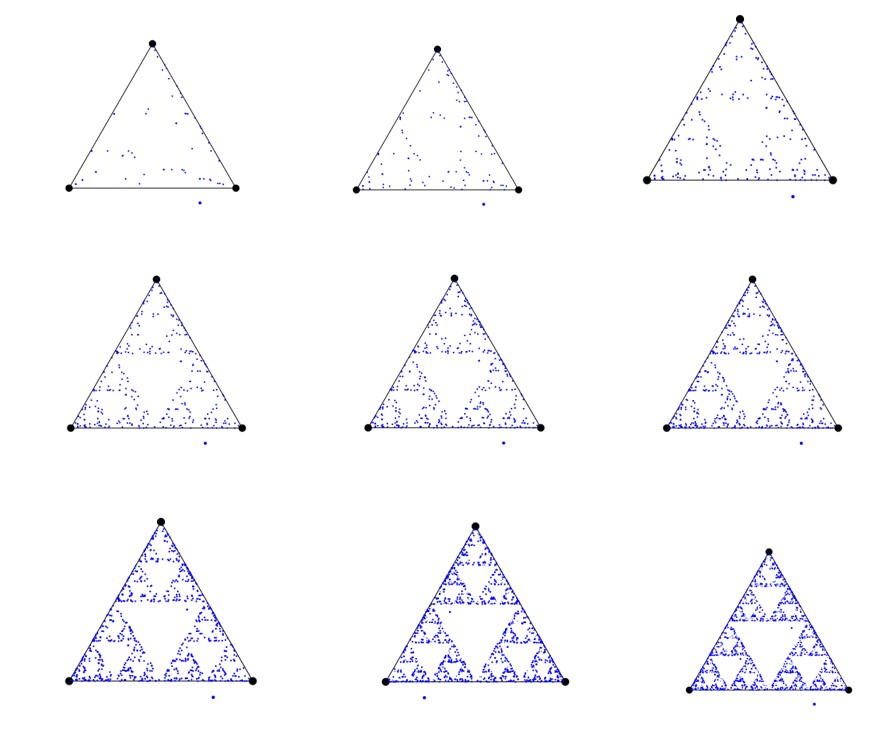
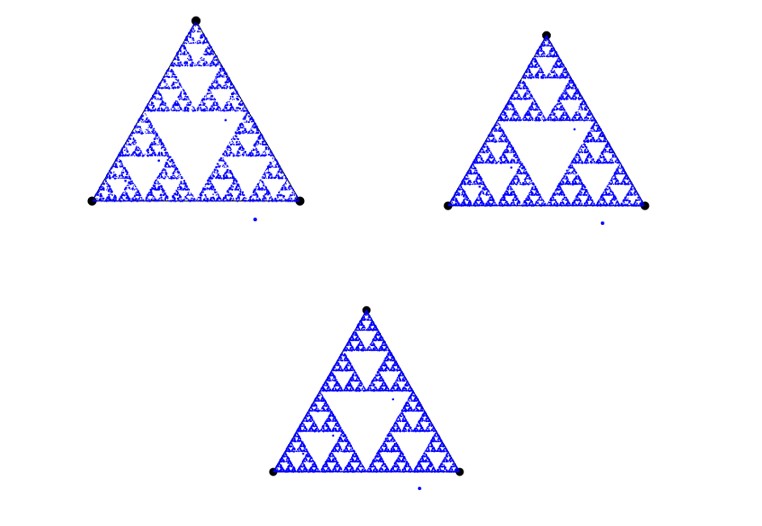
(Koniecznie przeczytajcie na końcu artykułu, kim tak ważnym był Wacław Sierpiński, że jego imieniem nazwano nawet krater na Księżycu!)
A więc już wiemy – z chaosu punktów wyłoniła się niespodziewanie figura znana jako trójkąt Sierpińskiego. Pora poznać właściwą definicję oraz konstrukcję tej fascynującej figury. Tym razem uzyskamy ją nie przez kropkowanie, a przez wycinanie.
Na początku mamy zwykły trójkąt równoboczny. Połączmy ze sobą środki boków trójkąta – w ten sposób duży trójkąt podzieli się na cztery mniejsze trójkąty, z których środkowy należy wyciąć – teraz figura składa się z trzech przystających do siebie mniejszych trójkątów równobocznych.
Możemy zauważyć, że każdy z tych małych trójkątów jest mniejszą kopią pierwotnego trójkąta. Analogicznie możemy więc podzielić każdy z nich na cztery trójkąty równoboczne i wyciąć środkowy – teraz figura będzie się składać z dziewięciu malutkich trójkątów.
Ten proces można kontynuować w nieskończoność, aż otrzymamy trójkąt Sierpińskiego – wycinankę, w której każda z mniejszych części jest pomniejszoną kopią całej figury. Ten „dziurawy trójkąt” oprócz tego, że wyłania się z gąszczu kropek w „grze w chaos”, ma mnóstwo ciekawych własności, które postaram się przybliżyć w tym artykule.
Wacław Sierpiński (ojciec figury) urodził się w 1882 roku w Warszawie. Ukończył V Gimnazjum Klasyczne, gdzie zainteresował się matematyką. Następnie rozpoczął studia na wydziale Fizyko-Matematycznym Cesarskiego Uniwersytetu Warszawskiego. Ukończył studia ze stopniem kandydata nauk i złotym medalem za pracę z teorii liczb, potem zyskał posadę nauczyciela matematyki i fizyki w IV Gimnazjum Żeńskim. Nie uczył jednak zbyt długo, bo po roku (w 1905) stracił pracę za udział w strajku szkolnym.
Wtedy wyjechał do Krakowa – tam polskość była bardziej akceptowana. Związał się z Uniwersytetem Jagiellońskim, gdzie napisał doktorat (na wydziale filozoficznym). Z matematyki zajmował się wtedy głównie teorią liczb – badał własności tzw. liczb Sierpińskiego. To takie nieparzyste liczby naturalne k, dla których wyrażenie k * 2^n + 1 nie jest liczbą pierwszą dla żadnej liczby naturalnej n. Wiele zagadnień z nimi związanych wciąż pozostaje problemami otwartymi.
Po kilku latach zajmowania się liczbami Sierpiński jednak zmienił temat badań. Zaintrygowało go twierdzenie mówiące, że można opisać punkty na płaszczyźnie tylko jedną współrzędną, a nie dwiema. Matematyk napisał list z zapytaniem o to, jak się wydawało dziwaczne, twierdzenie – w odpowiedzi przyszło podobno tylko jedno słowo: „Cantor”. To sprawiło, że Sierpiński zainteresował się zapoczątkowaną przez Georga Cantora teorią mnogości, zwaną też teorią zbiorów. Odtąd stała się jego ulubioną dziedziną.
Wrócił potem do Warszawy i kontynuował karierę nauczyciela w szkole średniej oraz wykładał matematykę na Wyższych Kursach Naukowych – odpowiedniku nieoficjalnego Uniwersytetu Polskiego w Warszawie. Habilitował się na Uniwersytecie Lwowskim – profesorem został w wieku 28 lat. Szybko zaczął tam wykładać teorię mnogości jako osobny przedmiot – jego kurs był jednym z pierwszych na świecie. Niedługo potem wydał swoje pierwsze książki. Badał swoje fraktale zanim jeszcze to pojęcie poznali inni matematycy – zdefiniował je dopiero później Benoit Mandelbrot.

W czasie wybuchu I wojny światowej przebywał na Białorusi, został internowany w Wiatce, ale dzięki wstawiennictwu moskiewskich matematyków zezwolono mu na przyjazd do Moskwy. Tam zajmował się dalszą pracą naukową, a swój I tom „Analizy Matematycznej” zadedykował Uniwersytetowi Polskiemu w Warszawie. W roku 1918 wrócił do Lwowa, a potem Warszawy.
Treścią życia Sierpińskiego była praca naukowa. Był raczej badaczem niż pedagogiem, ale starał się sumiennie wywiązywać ze swoich obowiązków dydaktycznych. Wspominając go w „Notatkach do autobiografii” inny wybitny warszawski matematyk, Kazimierz Kuratowski, pisał: „Nie był szczególnie komunikatywny (oczywiście w sprawach pozanaukowych). Przeciwnie, posiadał dar izolowania się od otaczającego świata; umysł jego pochłonięty był rozważaniem zagadnień matematycznych w czasie podróży w pociągu, w czasie posiedzeń Akademii, w czasie urzędowych obiadów czy kolacji”.
W roku 1920 Sierpiński wspólnie z Zygmuntem Janiszewskim i Stefanem Mazurkiewiczem założyli „Fundamenta Mathematicae” – czasopismo poświęcone teorii mnogości, jej zastosowaniom oraz logice matematycznej – było to pierwsze na świecie wyspecjalizowane czasopismo matematyczne. W czasie wojny polsko-bolszewickiej Sierpiński pracował w Wydziale Szyfrów Sztabu Głównego i przyczynił się do złamania sowieckiego szyfru wojskowego.
Podobno był orędownikiem liczenia od zera. Jak opowiadali jego przyjaciele, kiedyś na lotnisku Sierpiński zgłosił brak jednej z walizek.
– Ależ, Mr Sierpiński, są wszystkie. Sześć. Tyle pan wpisał w deklaracji, proszę jeszcze raz przeliczyć – tłumaczył personel.
– To niemożliwe – rozpaczał matematyk. – Liczyłem je już nieraz: zero, jeden, dwa, trzy, cztery, pięć…
W czasie niemieckiej okupacji nauczał na zajęciach konspiracyjnego uniwersytetu, co wtedy karane było śmiercią. W tym czasie otrzymał propozycję objęcia katedry na madryckim uniwersytecie – w bezpiecznej, neutralnej Hiszpanii. Odmówił.
Po wojnie powrócił do pracy na uczelni. Przez dwie dekady był prezesem Warszawskiego Towarzystwa Naukowego, a po jego likwidacji został jednym z trzech wiceprezesów Polskiej Akademii Nauk. Był jednym z sygnatariuszy Listu 34, który sprzeciwiał się cenzurze w PRL. Pod groźbą represji wycofał jednak później swoje poparcie dla tej inicjatywy.

Zmarł 9 października 1969. Pozostawił po sobie ponad 700 prac naukowych i ponad 60 książek i broszur. Cieszył się autorytetem w całej Europie. Tytułem profesora honoris causa obdarzyły go uniwersytety m.in. we Francji, Czechosłowacji, ZSRR, a jego imieniem nazwano krater na Księżycu. Został pochowany w Alei Zasłużonych na Cmentarzu Powązkowskim, a na jego nagrobku widnieje napis „Badacz nieskończoności”.

Czy jak będziemy w nieskończoność powtarzać procedurę wycinania środkowych trójkątów, to coś w ogóle z wyjściowego trójkąta zostanie? Coś na pewno, bo w ten sposób nigdy przecież nie wytniemy boków wyjściowego trójkąta. Jakby się głębiej zastanowić, to również boków trzech mniejszych trójkątów – i tak dalej. Zostanie całkiem dużo punktów, jednak na koniec okazuje się, że pozostała figura nie jest już właściwie figurą, tylko krzywą. Ma pole równe zero.
Ten fakt możemy dowieść na dwa sposoby. Pierwszy to klasyczne podobieństwo. Oznaczmy pole początkowego trójkąta jako P. Jeśli każdy z trzech pozostałych trójkątów jest do niego podobny, tylko dwa razy mniejszy, to pole jednego z nich powinno wynosić P/4. Początkowy trójkąt składa się z trzech takich trójkątów, więc jego pole to 3/4 P. Stąd P= 3/4 P. Stąd wynika wprost, że P=0.
To nic innego niż obliczenie granicy, do której zmierza pole otrzymywane po kolejnych etapach “wycinania”. Po pierwszym etapie usuwania pozostanie 3/4 początkowego pola. W następnym również usuniemy 1/4 z tego, co zostało , więc pozostanie 〖(3/4)〗^2 . I tak dalej, po następnym etapie pozostanie (3/4)^3, a po n-tym (3/4)^n początkowego pola. Jest to ciąg dążący do 0, czyli po nieskończenie wielu ruchach pole otrzymanej figury wynosi 0.
Podobnie możemy obliczyć obwód trójkąta Sierpińskiego. Przyjmijmy, że obwód początkowego trójkąta równobocznego wynosi Y. W pierwszym etapie wycinania zamieniamy go na trzy przystające trójkąty o dwa razy mniejszym obwodzie – czyli łączny obwód wyniesie 3/2 Y . Analogicznie po drugim etapie wycinania otrzymamy obwód (3/2)^2 Y. I tak dalej, po n-tym etapie łączny obwód będzie wynosił (3/2)^n Y. Granicą ciągu (3/2)^n jest nieskończoność, czyli obwód trójkąta będzie rósł do nieskończoności! Stąd “gotowy” trójkąt ma nieskończony obwód.
Co to za figura, która ma pole równe zero i nieskończony obwód, a mieści się wewnątrz trójkąta równobocznego? Własności trójkąta Sierpińskiego wymykają się klasycznej geometrii. Tego typu figury nazywamy fraktalami.
Słowo „fraktal” pochodzi od łacińskiego wyrazu fractus, który oznacza „złamany, cząstkowy, ułamkowy”. Potoczna definicja mówi o figurze, która jest podobna sama do siebie – całość jest taka sama, jak wycięta mniejsza część, a ta z kolei taka sama jak jeszcze mniejsza, i tak w nieskończoność. Tak jest z trójkątem Sierpińskiego – duży trójkąt jest taki sam jak każda z jego trzech niewyciętych części, te są takie same jak ich mniejsze części…
Trudno jest precyzyjnie zdefiniować pojęcie fraktala. Matematycy do warunku o samopodobieństwie dodają rozważania dotyczące wymiarów fraktalnych – spróbujmy więc wyznaczyć wymiar trójkąta Sierpińskiego. Narysowaliśmy go na płaszczyźnie, więc powinien być dwuwymiarowy. Z drugiej strony dowiedliśmy, że ma pole zero, jest tak naprawdę krzywą – to by wskazywało, że jego wymiar to jeden.
Jednym ze sposobów obliczania wymiaru figur jest zastanowienie się, ile podobnych do tej figury, mniejszych w skali k figur potrzeba, aby ją całą wypełnić. I tak dwa (jednowymiarowe) odcinki wystarczą do pokrycia jednego dwa razy dłuższego. Cztery kwadraciki pokryją kwadrat (dwuwymiarowy) o dwa razy większym boku, a osiem małych sześcianów (czyli trójwymiarowych figur) zmieści się w sześcianie o dwa razy większym boku.
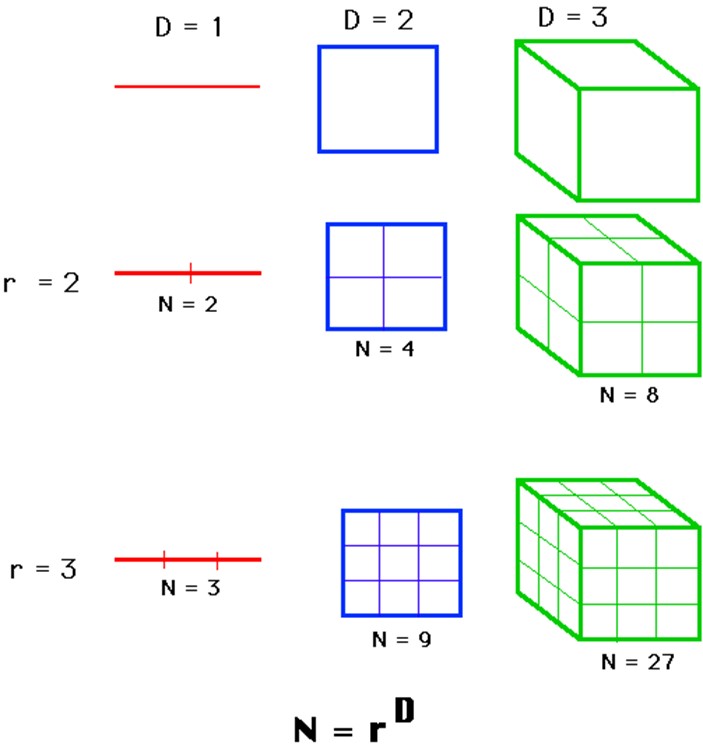
Stąd łatwo zauważyć pewien wzór:
Spróbujmy w ten sposób obliczyć wymiar trójkąta Sierpińskiego – oznaczmy go jako x. Trójkąty, na które go dzielimy, mają dwa razy mniejszy bok od wyjściowego trójkąta, czyli skala podobieństwa wynosi 2. Za to mieści się ich w dużym trójkącie trzy. Stąd 2^x=3, czyli wymiar trójkąta Sierpińskiego wynosi x= $log_2$ (3)≈1,585…. Ale przecież to jest liczba niecałkowita, a nawet niewymierna! Okazuje się więc, że istnieją figury, których wymiar nie jest liczbą całkowitą. „Nietypowość” obliczonego w ten sposób wymiaru oraz samopodobieństwo to główne kryteria uznania czegoś za fraktal.
Pora na krótkie wyjaśnienie, a właściwie zarys dowodu – dociekliwych czytelników odsyłam do tej anglojęzycznej strony https://arun.chagantys.org/technical/2020/04/28/chaos-game.html, gdzie można znaleźć szczegółowy dowód na to, że niezależnie od wyboru początkowego punktu zawsze wygeneruje się trójkąt Sierpińskiego oraz animacje jego powstawania i kolejnych etapów dowodu.
Najpierw należy udowodnić, że jeśli gra w chaos przekształci punkt należący do trójkąta Sierpińskiego w inny punkt również należący do niego – to jest, jeśli pewien punkt $P_k$ należy do trójkąta Sierpińskiego, to punkt $P_ (k+1)$ również do niego należy. To oznacza, że jeśli mamy szczęście i na samym początku wybierzemy punkt $P_0$ należący już do tej figury – gra w chaos wygeneruje trójkąt Sierpińskiego idealnie, bez żadnych obcych punktów. Aby dowieść ten fakt, załóżmy bez straty ogólności, że w tym kroku wylosowaliśmy wierzchołek A. Rozważmy jednokładność o środku w punkcie A i skali 1/2 – punkt $P_(k+1)$ jest po prostu obrazem punktu $P_k$ w tej jednokładności. Jednocześnie ta sama jednokładność przekształca cały, duży trójkąt Sierpińskiego na jedną z jego trzech bliźniaczych części – tę przy wierzchołku A. Czyli jeśli punkt $P_k$ leżał gdzieś wewnątrz dużego trójkąta, to punkt $P_(k+1)$ będzie leżał w dokładnie tym samym miejscu mniejszej kopii trójkąta – czyli również na nim.
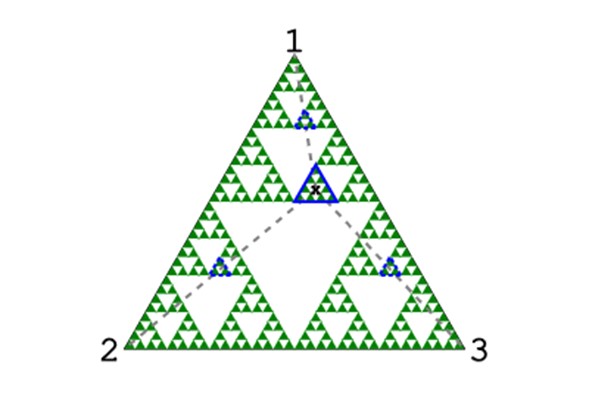
Udowodnię, że w każdym kroku gry w chaos punkt $P_(k+1)$ znajdzie się co najmniej o połowę bliżej trójkąta Sierpińskiego, niż punkt $P_k$. Aby to dowieść, przypiszmy każdemu punktowi $P_k$ jego „punkt bliźniaczy” $Q_k$ – będzie to najbliższy do punktu $P_k$ punkt, który należy do trójkąta Sierpińskiego. Rozważmy teraz tę samą jednokładność, co w poprzednim akapicie – łatwo dowieść, że punkt $Q_(k+1)$ to nic innego, jak obraz punktu $Q_k$ w tej jednokładności. Ponieważ $P_(k+1)$ to również obraz punktu $P_k$ w tej jednokładności, odległość między punktami $P_(k+1)$ i $Q_(k+1)$ będzie o połowę mniejsza, niż między punktami $P_k$ i $Q_k$. To oznacza, że każdy kolejny punkt P będzie coraz bliżej trójkąta Sierpińskiego i ta odległość zmniejsza się szybko – po kilku krokach punkty $P_k$ i $Q_k$ są praktycznie nieodróżnialne dla ludzkiego oka.
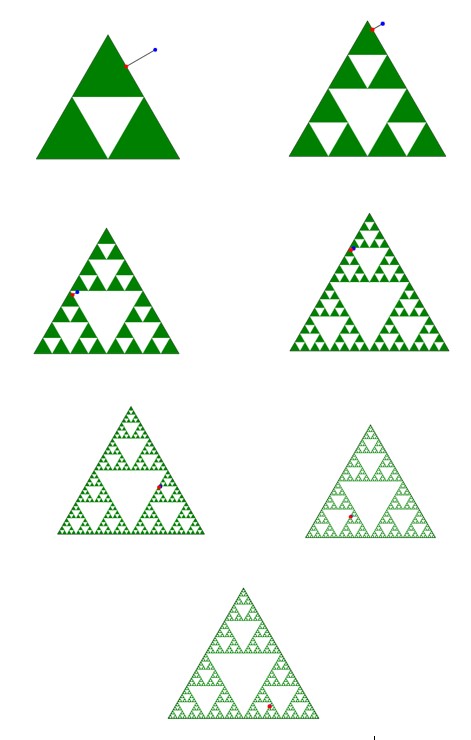
Ostatni etap dowodu to pokazanie, że wszystkie punkty trójkąta Sierpińskiego zostaną kiedyś odwiedzone – a dokładniej, że po pewnej, skończonej liczbie kroków dojdziemy dowolnie blisko do każdego punktu należącego do trójkąta Sierpińskiego. Ten etap dowodu jest znacznie trudniejszy od poprzednich, dlatego przedstawię tylko jego zarys. Etap ten pokazuje, że znajdziemy się dowolnie blisko każdego punktu trójkąta Sierpińskiego – formalnie rzecz biorąc, dla każdego punktu należącego do trójkąta Sierpińskiego i każdej, dowolnie małej liczby ε prawdopodobieństwo, że w którymś kroku znajdziemy się w odległości mniejszej od ε od tego punktu, dąży do 1. W tym celu każdemu z niewyciętych trójkątów nadajemy „numer identyfikacyjny” w postaci ciągu liczb i analizując własności tych ciągów obliczamy prawdopodobieństwo, że znajdziemy się w pewnym bardzo malutkim trójkąciku, w którym wszystkie punkty są bardzo blisko żądanego punktu. Dokładny opis tego etapu znajduje się w podanym przeze mnie linku.
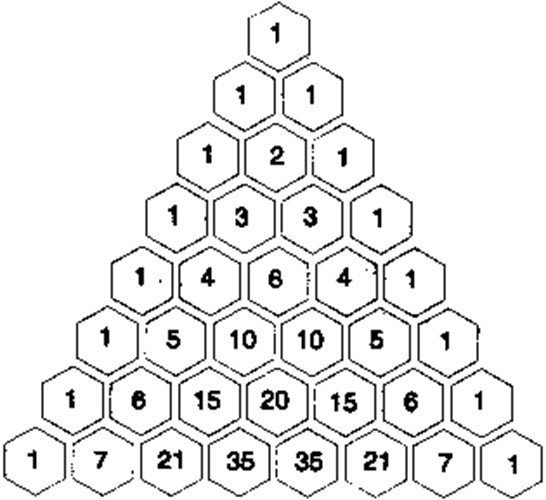
To znaczy, w pierwszym rzędzie jest tylko jedynka (czyli (1¦1) ), w drugim dwie liczby (2¦1) i (2¦2), w trzeci trzy liczby (3¦1), (3¦2) i (3¦3). I tak dalej, w n-tym rzędzie znajdziemy liczby (n¦1), (n¦2), (n¦3), …, (n¦n). Trójkąt Pascala możemy też otrzymać po prostu pisząc na jego brzegach jedynki, a w pozostałych polach sumę dwóch liczb, które są nad nimi.
No dobrze, trójkąt Pascala jest przydatny w życiu (na przykład przy rozpisywaniu dwumianu (x+y)^n, ale co właściwie ma wspólnego z trójkątem Sierpińskiego?
Pokolorujmy teraz trójkąt Pascala – liczby nieparzyste na czarno, a liczby parzyste na biało. Po jakimś czasie pokaże się… Co? Trójkąt Sierpińskiego! Oczywiście nie ten z nieskończenie małymi dziurami, bo w końcu miejsca zajęte przez liczby mają pewien swój rozmiar, ale im dalej rozpiszemy i pokolorujemy trójkąt Pascala, tym dokładniejszym trójkątem Sierpińskiego on będzie.
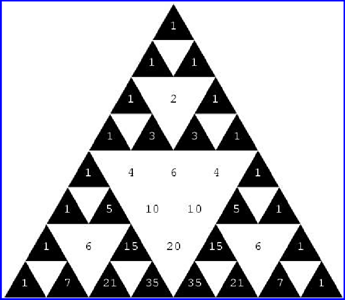
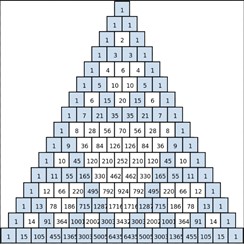
Aby tego dowieść, wystarczy pokazać, że za każdym rozszerzeniem rozpisanego trójkąta Pascala dwukrotnie okazuje się, że „górny” trójkąt skopiuje się do „prawego” i „lewego” (dowiedziemy to osobno dla każdej liczby z niego), a „środkowy” trójkąt pozostanie pokolorowany na biało (czyli wypełniony nieparzystymi liczbami). Tak naprawdę wystarczy pokazać, że „środkowy”, wycięty trójkąt ma górny rządek składający się z liczb parzystych oraz nieparzyste końce. W ten sposób w każdym kolejnym rzędzie otrzymamy o jeden krótszy rządek liczb parzystych, ponieważ każda liczba trójkąta Pascala jest sumą dwóch wyższych liczb. W efekcie powstanie obrócony „do góry nogami” trójkąt równoboczny złożony z parzystych liczb – środkowy wycięty trójkąt
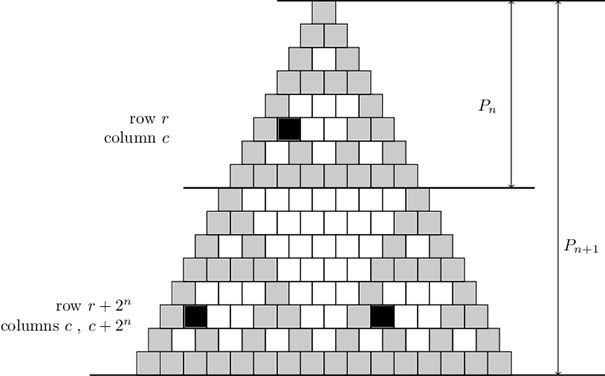
Jest to równoważne z pokazaniem, że dla każdego całkowitego 0≤r<2^n oraz 0 ≤c ≤r (r to numer rzędu, a c numer kolumny) zachodzi następujące przystawanie:
(r¦c) ≡ ((r+2^n)¦c) ≡((r+2^n)¦(c+2^n ))(mod 2)
(To dowodzi, że górny trójkąt kopiuje się do prawego i lewego)
Oraz dla każdego całkowitego 1≤c≤2^n-1 zachodzi:
(2^n¦c) ≡ 0 (mod 2)
(To dowodzi, że powstanie górny rządek pustego, środkowego trójkąta – wiemy, że jego brzegi będą liczbami nieparzystymi, gdyż są to liczby (2^n¦0) =(2^n¦2^n )=1 )
Te przystawania możemy pokazać między innymi wykorzystując twierdzenie Lucasa – pełny dowód tego twierdzenia i wielu rozszerzeń znajduje się w anglojęzycznej pracy naukowej pod tym linkiem: https://arxiv.org/pdf/1708.07429.pdf.
Trójkąt Sierpińskiego wyłania się nie tylko z „gry w chaos” i trójkąta Pascala – ujrzysz go także na każdej kartce z treściami zadań Olimpiady Matematycznej.
Dlatego myślę, że warto o nim wiedzieć coś więcej – w końcu to w niego będziesz się wpatrywać przez pięć godzin, jeśli przejdziesz do etapu okręgowego Olimpiady. Mam nadzieję, że po przeczytaniu tego artykułu przyznasz, że Olimpiada nieprzypadkowo wybrała tę fascynującą figurę na swoje logo – w końcu jest ona pięknym przykładem elegancji i „zaskakującości” matematyki.
Zachęcam Cię również do dołączenia do prowadzonych przeze mnie przygotowań olimpijskich! Szczegóły kursu przygotowującego do Olimpiady Matematycznej znajdziesz pod tym linkiem.
Autor tekstu: Jagoda Bracha
1. Wikipedia
2. https://arxiv.org/pdf/1708.07429.pdf – dowód własności trójkąta Pascala
3. https://arun.chagantys.org/technical/2020/04/28/chaos-game.html – dowód własności gry w chaos (bardzo dopracowany artykuł w języku angielskim, wart przeczytania!)
4. http://www.jrm2019.pl/fraktal-na-100-lecie/trojkatsierpinskiego/
5. http://www.math.uni.wroc.pl/~elakalin/Prezentacja%20fraktale.pdf?fbclid=IwAR0W1h1hgKcmnEre4xwpkpXAdJYKsZdtM6CWq6pmHB4YtyO8tLxa_10RP80
1. https://www.ipsb.nina.gov.pl/a/biografia/waclaw-franciszek-sierpinski
2.https://bialczynski.pl/2015/08/20/wielcy-polacy-waclaw-sierpinski-1882-1969-genialny-matematyk/
3. https://www.polskieradio.pl/39/156/Artykul/1738959,Waclaw-Sierpinski-%e2%80%93-badacz-zagadek-nieskonczonosci
4. https://wyborcza.pl/AkcjeSpecjalne/7,160474,24501452,zaczynali-od-zera-stali-sie-legenda-jak-warszawscy-matematycy.html
1. Powstawanie trójkąta z gry w chaos – https://arun.chagantys.org/technical/2020/04/28/chaos-game.html
2. Konstrukcja trójkąta Sierpińskiego – https://254155-841844-raikfcquaxqncofqfm.stackpathdns.com/wp-content/uploads/2017/04/Sierpinski-gasket-or-triangle-fractal-collapse.jpg
3. Wytłumaczenie wymiaru fraktalnego – https://upload.wikimedia.org/wikipedia/commons/thumb/4/4d/Fractaldimensionexample.PNG/220px-Fractaldimensionexample.PNG
4. Dowód własności gry w chaos – https://arun.chagantys.org/technical/2020/04/28/chaos-game.html
5. Trójkąt Pascala – https://staticbryk.iplsc.com/bryk_prod_2017_08/00021855.gif
6. Pokolorowany trójkąt Pascala – https://www.researchgate.net/profile/Klee_Irwin2/publication/314209738/figure/fig10/AS:832150756671489@1575411609516/Sierpinski-triangle-showing-Pascal-triangle-values.png i https://fractalfoundation.org/wp-content/uploads/2018/11/PascalsFractalTriangle-Answers.jpg
7. Dowód własności trójkąta Pascala – https://arxiv.org/pdf/1708.07429.pdf
8. Logo Olimpiady Matematycznej
9. Portrety Wacława Sierpińskiego – https://liceum.slupsk.pl/wordpress/wp-content/uploads/2014/12/waclaw_sierpisnki.jpg i https://sites.google.com/site/pascalsierpinskifibonacci/_/rsrc/1468742266095/waclaw-sierpinski/sierpinski%203.jpg?height=200&width=159

Strona przygotowana przez Zyskowni.pl