Zasada Fermata jest bardzo pożytecznym narzędziem do rozwiązywania zadań z optyki na Olimpiadzie Fizycznej. Pozwala w sposób elegancki i stosunkowo zwarty rozwiązać problemy olimpijskie, które wymagają śledzenia wielu promieni świetlnych na raz. Jeśli chcesz poznać inne techniki rozwiązywania takich zadań, zapraszam na kurs Indeksu w Kieszeni!
www.pexels.com
Zasadę Fermata sformułować można w prosty sposób:
„Promień świetlny porusza się po takim torze, dla którego czas ruchu jest minimalny”.
Nie jest to najogólniejsze z możliwych jej sformułowań, bo jeśli odpowiednio długo się pomyśli, można też znaleźć przykłady, dla których czas jest maksymalny lub niezmienny względem małych odkształceń toru. Na wszystkie przypadki razem wzięte (minimalny, maksymalny i niezmienny względem małych odkształceń) istnieje jedno mądre słowo: „stacjonarny”. Trafniejszym sformułowaniem zasady Fermata jest zatem zdanie:
„Promień świetlny porusza się po takim torze, dla którego czas ruchu jest stacjonarny”.
Skoro już poznaliśmy brzmienie zasady Fermata, trzeba zabrać się za wyjaśnienie pojęć użytych do jej sformułowania:
– promień świetlny to krzywa zadana przez warunek prostopadłości do powierzchni stałej fazy fali. Oznacza to, że jeśli fala ma grzbiety, to promień będzie krzywą w każdym miejscu do grzbietów prostopadła. Ostatecznie koń, jaki jest – każdy widzi;
– tor to krzywa składająca się z kolejnych położeń czegoś w przestrzeni.
W jednorodnej przestrzeni (izotropowej – kolejne trudne, ale dość użyteczne słowo), w której każdy kierunek „wygląda” tak samo, światło, jak wiadomo, porusza się po prostej. Zasada fermata ten fakt odtwarza. Z definicji pojęcia prostej jest to najkrótsza droga, którą trzeba przebyć, żeby dostać się z punktu A do B. Jako że w przypadku przestrzeni, w której prędkość poruszania się nie zależy od miejsca, żeby policzyć czas znając drogę, wystarczy podzielić przez prędkość, prosta będzie minimalizować czas ruchu.
Skoro już ustaliliśmy, że prosta jest prosta, rozważmy ciekawszy przypadek. Załóżmy, że analizowany promień od czegoś się odbija. Ponadto przyjmijmy, że jeśli kąt padania to α to kąt odbicia to β.
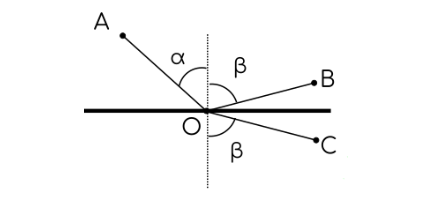
Odcinek OC został narysowany poprzez symetryczne odbicie względem lustra odcinka OB. Długość odcinka |OC| jest oczywiście taka sama jak |OB|. Płynie z tego wniosek, że droga od A do C po odcinkach AO i OC ma taką samą długość jak droga od A do B po odcinkach AO i OC. Zatem, skoro jedna jest minimalna, to druga również musi być minimalna. Dość łatwo natomiast jest zauważyć, że długość toru od A do C (zatem i od A do B) jest minimalna, gdy punkty A, O i C leżą jednej prostej, czyli gdy α = β. Warunek minimalizacji drogi oczywiście i w tym przypadku odpowiada minimalnemu czasowi, co oznacza, że kąt padania w istocie jest równy kątowi odbicia.
Wyprowadziliśmy zatem prawo odbicia z zasady Fermata. Uwzględniając fakt, że prędkość światła jest różna w różnych ośrodkach, można wychodząc od zasady Fermata udowodnić również prawo załamania. Wymaga to jednak użycia pochodnych. Odsyłam w tym celu do następującego źródła: https://pl.wikipedia.org/wiki/Zasada_Fermata
To jednak było zbyt proste i elementarne jak na zadanie olimpijskie. Spróbujmy rozwiązać zadanie o porównywalnej trudności co zadanie teoretyczne na II bądź III etapie olimpiady.
Naszym zadaniem jest skonstruować soczewkę o ogniskowej f, która będzie miała obie powierzchnie płaskie. Zakładamy, że grubość naszej soczewki to d<<f. Współczynnik załamania materiału soczewki n(r) zależy od odległości r od jej środka. Naszym celem jest znalezienie funkcji n(r).
Okazuje się, że promień świetlny, mimo że nie załamuje się jak w klasycznej soczewce, to na skutek występowania gradientu współczynnika załamania zostanie odchylony. Dość dobrą demonstrację tego zjawiska można zobaczyć tutaj: Refractive Properties of Gradient Index Optics
Przybliżenie cienkiej soczewki d<<f potrzebne jest, aby móc ustalić czas podróżowania prostopadłego do soczewki promienia jako:
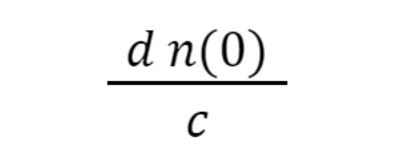
W celu rozwiązania zadania udowodnię najpierw lemat.
Dla dowolnego trójkąta, jeśli obierzemy jeden z wierzchołków oraz odpowiadającą mu podstawę (leżącą naprzeciwko) i będziemy modyfikować ten trójkąt w taki sposób, że oddalamy wybrany wierzchołek po prostej prostopadłej do wybranej podstawy, to, w granicy nieskończonego oddalenia, długości boków trójkąta przylegające do wybranego wierzchołka są sobie równe.
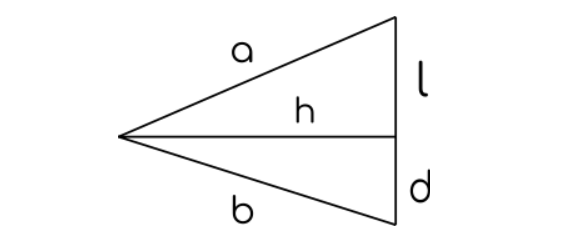
Żeby udowodnić lemat wystarczy pokazać że:
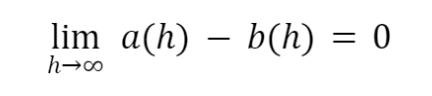
Korzystając z twierdzenia Pitagorasa:
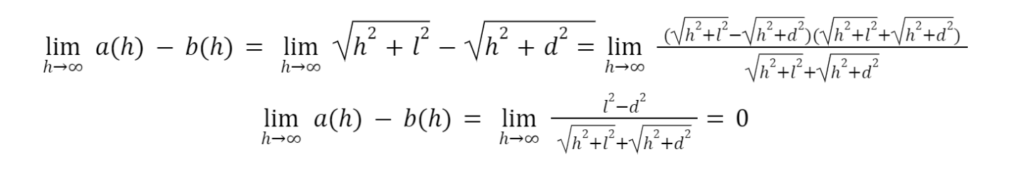
Ostatnia równość wynika z tego, że mianownik dąży oczywiście do nieskończoności a licznik to jakaś stała. Dowód lematu zakończony – czas zatem na właściwe zadanie.
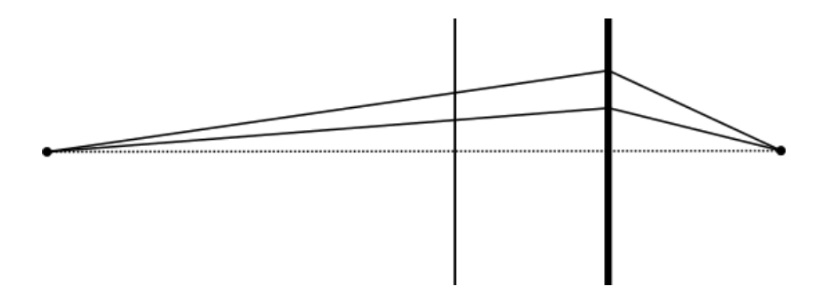
Żeby rozwiązać zadanie załóżmy na początek, że chcemy ogniskować nie promienie równoległe, lecz wychodzące z jednego punktu. Jeśli wszystkie mają trafiać w ognisko za soczewką, to z zasady Fermata każdy z „rozsądnych” torów musi odpowiadać czasowi stacjonarnemu. Torem „rozsądnym” możemy nazwać taki, jak te narysowane. Skoro wszystkie mają spełniać ten warunek, to dla każdej „rozsądnej” drogi trafiającej w soczewkę czas lotu od źródła do ogniska musi być identyczny.
Jeśli oddalimy źródło do nieskończoności, to promienie z niego wychodzące, a trafiające w soczewkę, staną się równoległe. Obierzmy dodatkowo jakąś płaszczyznę w skończonej odległości od soczewki. Na podstawie lematu droga od źródła położonego w nieskończoności do dowolnego miejsca na tej płaszczyźnie, znajdującego się w skończonej odległości od osi optycznej, jest identyczna. Zatem czas lotu od źródła do tego miejsca jest identyczny.
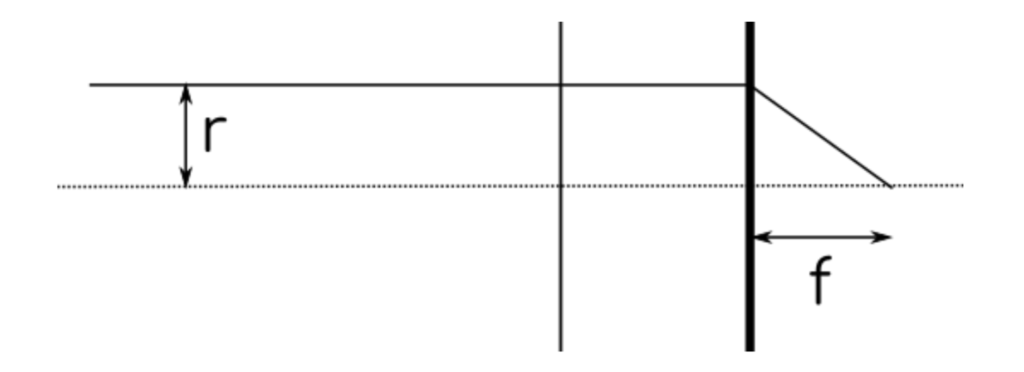
Zatem, aby soczewka ogniskowała, czas lotu od owej płaszczyzny do ogniska musi być identyczny i równy pewnej stałej T. Jest ona zależna od współczynnika załamania w środku soczewki, odległości płaszczyzny od soczewki D oraz od ogniskowej f.
Możemy zatem zapisać równanie na czas lotu od płaszczyzny do ogniska f.
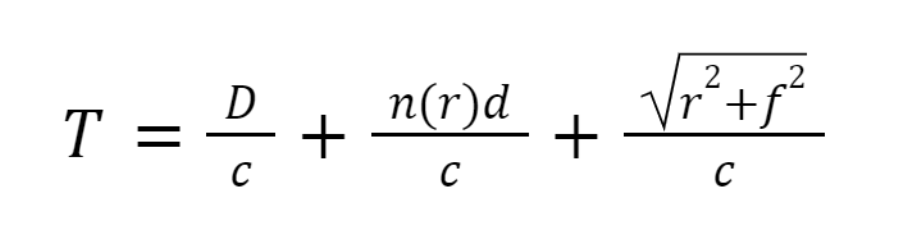
Stałą D możemy ustalić jako zero (czyli płaszczyzna leży na początku soczewki). Obliczamy zatem końcowy wynik:
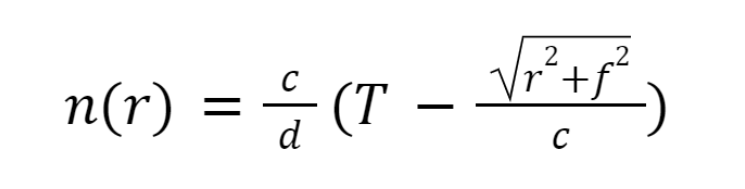
Stała T natomiast, jak łatwo zauważyć, jest równa:
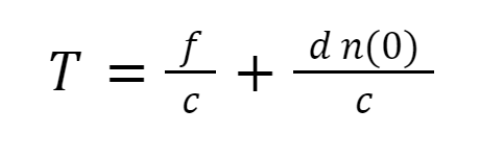
Na tym kończy się ten krótki materiał. Szukasz więcej ciekawych problemów oraz świetnych materiałów ułatwiających przygotowanie do Olimpiady Fizycznej? Nie zapomnij zapoznać się z ofertą przygotowaną przed Indeks w Kieszeni!
Strona przygotowana przez Zyskowni.pl
Zakładamy Ci konto na naszej platformie e-learningowej, na której znajdują się materiały, artykuły popularnonaukowe, czy nagrania video! Możesz tam bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane do sprawdzenia prace.
Na platformie otrzymujesz moduły - zestawy materiałów z prezentacjami, skryptami, testami, kartkówkami. Z nimi pracujesz w dowolnym miejscu - w domu, w podróży, w bibliotece.
Na platformie, gdzie odbywa się kurs możesz zadawać pytania 24h na dobę 7 dni w tygodniu - Prowadzący są tam po to by zawsze Ci pomóc i rozwiać Twoje wątpliwości.
Twój progres w nauce jest kontrolowany wraz z każdym kolejnym modułem - służą temu wszelkie kartkówki, testy i sprawdziany, które rozwiązane odsyłasz i otrzymujesz szczegółowy klucz.
Celujesz w świetny wynik na egzaminie ósmoklasisty? A może potrzebujesz tylko usystematyzować posiadaną wiedzę? Nieważne - nasz kurs (tempo pracy i materiały oraz pomoc Prowadzącego) jest zawsze dopasowany do aktualnego stanu Twoich umiejętności i oczekiwań.
Na platformie otrzymasz nielimitowany w okresie przygotowań dostęp do nagrań video, na których nasz zespół merytoryczny przeprowadzi Cię przez najbardziej wymagające i najczęściej pojawiające się na arkuszu zagadnienia egzaminacyjne.
Indywidualny kurs e-learningowy
egzamin ósmoklasisty
Wolisz uczyć się we własnym tempie i na własnych zasadach? W takim razie kurs e-learningowy jest stworzony właśnie dla Ciebie!
Nowoczesna forma indywidualnej nauki zdalnej (start: natychmiast lub we wskazanym terminie)
Dostęp do dedykowanej platformy do nauki e-learningowej
Harmonogram przygotowań dostosowany do dostępności ucznia
Przypisany opiekun merytoryczny prowadzący kurs
Komplet materiałów podzielonych na moduły tematyczne, a w każdym z nich: prezentacje, testy, kartkówki, skrypty, karty pracy i zadania egzaminacyjne
Materiały video – do kursu dołączone są nagrania video, na których członkowie zespołu merytorycznego IWK tłumaczą najtrudniejsze lub najbardziej prawdopodobne w wystąpieniu na egzaminie zagadnienia
Indywidualne podejście – otrzymujesz dostęp do naszej dedykowanej platformy edukacyjnej z pomocami naukowymi, na której możesz bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane prace.
Regularnie sprawdzane postępy
Ciągła możliwość kontaktu z Prowadzącym
Dzięki nowoczesnej formie nauki nasze kursy są dostępne dla uczniów z całej Polski – możesz dołączyć do nich niezależnie od miejsca zamieszkania i zacząć przygotowania już dziś! Skontaktuj się z nami i nie odkładaj decyzji na później – do egzaminu ósmoklasisty coraz bliżej!
Grupowy kurs całoroczny
egzamin ósmoklasisty
Chcesz solidnie przygotować się do egzaminu ósmoklasisty? Wolisz regularne zajęcia w grupie i stałe wsparcie prowadzącego? Jeśli tak, kurs grupowy będzie idealnym wyborem dla Ciebie!
46 godzin lekcyjnych zajęć (23 spotkania) + prace domowe
Forma stacjonarna (w salach w Warszawie) lub webinarowa (zajęcia online na żywo)
Nagrania z zajęć webinarowych oraz nagrania umożliwiające nadrobienie materiału osobom zapisującym się po rozpoczęciu kursów stacjonarnych
Możliwość wyboru grupy zajęciowej (harmonogram pojawi się w lipcu 2026 r.)
Pomoc pomiędzy zajęciami – ciągła możliwość kontaktu z Prowadzącym przez dedykowaną grupę zajęciową
Materiały z zajęć w formie cyfrowej
Regularne zajęcia pomagają utrzymać systematyczność w nauce i realnie wpływają na lepsze wyniki na egzaminie ósmoklasisty. Co roku wielu naszych uczniów z różnych części Polski osiąga wysokie rezultaty. Zapisz się na zajęcia już dziś i przygotuj się z nami do egzaminu ósmoklasisty!