

Zaraz zapoznasz się z artykułem przygotowanym przez jednego z naszych Prowadzących kurs do Olimpiady Matematycznej. Jest to skuteczna i rozwijana od ponad 10 lat metoda nauki, która co roku umożliwia naszym Podopiecznym osiąganie sukcesów na finale! Po zakończonej lekturze koniecznie zapoznaj się ze szczegółami na dedykowanej podstronie.
Bardziej doświadczeni olimpijczycy z pewnością znają Zasadę Szufladkową Dirichleta (i mogą śmiało przejść kilka akapitów do przodu). Dla tych, którzy swoją przygodę z Olimpiadą dopiero zaczynają, nakreślę szybko jej treść. Jest to po prostu stwierdzenie mówiące, że jeśli pewną liczbę obiektów próbujemy umieścić w mniejszej od niej liczbie szufladek, to w pewnej szufladce muszą znaleźć się przynajmniej dwa obiekty. Oczywiście w miejsce słów „obiekty”, „szufladki” oraz „umieścić” możemy wstawić dowolne inne określenia nadające powyższemu zdaniu sens. Jeśli więc naszymi obiektami będzie osiem osób a szufladkami dni tygodnia, w których będziemy umieszczać te osoby. Przykładowo na podstawie tego, którego dnia się urodziły, to otrzymamy wówczas stwierdzenie, że wśród dowolnej grupy ośmiu osób znajdziemy dwie urodzone tego samego dnia tygodnia.
Wymienione przed chwilą stwierdzenie (jak i cała Zasada) nie brzmią zbyt skomplikowanie. Oczywiście takie nie są – ich dowód nie jest bowiem niezbyt zawiły i dość intuicyjny (z formalnego punktu widzenia przeprowadza się go najczęściej nie wprost – zachęcam do jego przeprowadzenia w ramach ćwiczeń). Zasada Szufladkowa Dirichleta (ZSD) doczekała się swojej własnej nazwy głównie dlatego, że jest „schematem myślowym”, do którego łatwo możemy się odwołać w trakcie rozwiązywania zadania. Jest to po prostu konstrukcja ułatwiająca nam przeprowadzenie i napisanie rozumowania, a sprawdzającemu sprawdzenie jego poprawności – czyni rozwiązanie bardziej przejrzystym. Nie jest to jednak nigdy samodzielna technika rozwiązywania zadań i zawsze idzie w parze z jakimś dodatkowym rozumowaniem, a w zasadzie to ona sama jest często jedynie dodatkiem.
Spójrzmy na trójkąt równoboczny o boku 1. Obiektami niech będą jego wierzchołki (3), a szufladkami kolory (2). Na mocy ZSD otrzymujemy, że pewne dwa obiekty będą w tej samej szufladce, co tłumaczy się jako: pewne dwa wierzchołki będą tego samego koloru. A skoro są odległe o 1 (jak to w trójkącie równobocznym o boku 1 bywa), to nasze zadanie jest zakończone.
Jak widzimy, w treści zadania nie ma nic, co mogłoby w oczywisty sposób sugerować skorzystanie z ZSD. Patrząc na zadanie i ogrom możliwości (mamy w końcu płaszczyznę pokolorowaną w dowolny sposób dwoma kolorami; trudno jest sobie nawet wyobrazić, jak miałoby to wyglądać), dochodzimy do wniosku, że należy się skupić jedynie na małym podzbiorze punktów płaszczyzny i próbować na nim przeprowadzić jakieś rozumowanie. W ten sposób możemy trafić na rozwiązanie zbliżone do powyższego. Użycie Zasady nasuwa się samo – można byłoby o niej nie wspominać, ale jej użycie nadaje rozwiązaniu intuicyjnego sensu. Spróbujmy czegoś trudniejszego:
Liczba kończy się dziesięcioma zerami wtedy i tylko wtedy, gdy jest niezerowa i podzielna przez 10^10. Będziemy więc rozpatrywać jedynie reszty z dzielenia wyrazów ciągu Fibonacciego przez tę właśnie liczbę. Znając reszty dowolnych dwóch sąsiednich wyrazów jesteśmy w stanie wyznaczyć reszty wszystkich następnych (jak i poprzednich – będzie to istotne później), stąd jeśli w pewnym momencie dowolna para reszt powtórzy się, to cały ciąg reszt się zapętli. To jednak musi nastąpić, ponieważ ciąg ma nieskończenie wiele wyrazów, a jest tylko skończenie wiele par reszt z dzielenia przez 10^10 (dokładniej jest ich 10^20). Tak jak wspomnieliśmy wcześniej, patrząc wstecz do reszt poprzednich wyrazów dochodzimy do wniosku, że każda taka „pętla” musi zawierać tę samą resztę z dzielenia przez 10^10, F_0=0. Dowodzi to, że istnieje nawet nieskończenie wiele takich wyrazów.
Można zadać pytanie, w którym momencie skorzystaliśmy z Zasady Szufladkowej Dirichleta, nie wspominamy o niej przecież ani razu. Odwołujemy się do niej pośrednio w zdaniu „To jednak musi nastąpić, ponieważ ciąg ma nieskończenie wiele wyrazów, a jest tylko skończenie wiele par reszt z dzielenia przez 10^10” – stosujemy tu tzw. „nieskończoną ZSD”, gdzie mamy nieskończenie wiele obiektów, a jedynie skończenie wiele szufladek. Widzimy więc, że nie zawsze musimy się do Zasady odwoływać w sposób dosłowny, niemniej jednak wciąż dobrze jest mieć z tyłu głowy, że z niej korzystamy. Dla ciekawych dodam jedynie, że długość takiej „pętli” nazywa się okresem Pisano (Leonardo Pisano to właśnie Fibonacci). Gdy liczba, której reszty z dzielenia rozpatrujemy jest równa 10^10 okres ten ma długość 1.5∙10^10 (można to sprawdzić patrząc na ciąg A096363 w OEIS). Popatrzmy teraz na zadanie, w którym użycie ZSD jest oczywiste, jednak na pierwszy rzut oka nie wiadomo, do czego ją zastosować
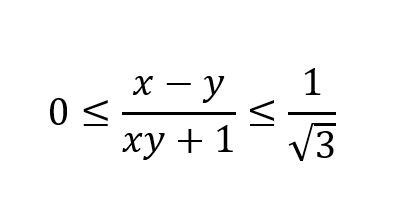
Zadanie można de facto rozwiązać tylko w jeden sposób. Aby wpaść na to rozwiązanie trzeba być dobrze zaznajomionym z trygonometrią. Należy bowiem w powyższym wyrażeniu dostrzec wzór na tangens różnicy. Korzystając z faktu, że tangens (ograniczony do przedziału [-π/2,π/2]) jest suriekcją (tj. przyjmuje wszystkie wartości rzeczywiste) możemy każdej tych siedmiu liczb przyporządkować jedną z powyższego przedziału, tak by jej tangens był jej równy. Wówczas wśród tej siódemki nowych liczb mamy znaleźć taką dwójkę, która spełnia nierówność:
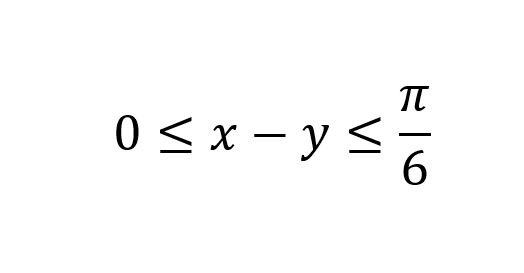
A to już proste zastosowanie Zasady Szufladkowej Dirichleta.
Zadań, w których ZSD znajduje zastosowanie jest naprawdę wiele. Wśród nich można jednak wyodrębnić dwie całkiem spore grupy. Pierwszą z nich są zadania związane z liczbami niewymiernymi – najbardziej klasycznym jest wykazanie, że dla każdej liczby rzeczywistej x z przedziału [0,1] i dowolnej liczby niewymiernej α, i dowolnie małej liczby rzeczywistej ε>0, istnieje takie naturalne n, że część ułamkowa liczby nα jest odległa od x o nie więcej niż ε (można pokazać nawet więcej – ciąg części ułamkowych liczb nα jest równomiernie rozłożony na przedziale [0,1], nie jest to jednak proste do udowodnienia biorąc pod uwagę, że trudno nawet zdefiniować, co „równomiernie rozłożony” oznacza).
Drugą grupą są różnego rodzaju zadania geometryczne – wykazywanie, że w pewnej grupie punktów wewnątrz jakiegoś obiektu znajdują się dwa oddalone o nie więcej niż pewna wartość. Tutaj wyzwaniem jest odpowiednie dobranie szufladek, tzn podzielenie zadanego obszaru na mniejszą liczbę części niż jest punktów w zadaniu tak, by w każdym obszarze dowolne dwa punkty były dostatecznie blisko siebie.
Na koniec zostawiam Cię z kilkoma zadaniami do samodzielnego rozwiązania. Ich poziom trudności sięga od stosunkowo prostych do dość trudnych – powodzenia!
Zadanie IV
Ile osób potrzeba, by mieć pewność, że pewne trzy urodziły się tego samego dnia tygodnia i tego samego miesiąca?
Zadanie V
Liczby pierwsze p, q, r są większe od 3. Pokaż, że 48|(a − b)(b − c)(c − a).
Zadanie VI
Ze zbioru {1,2,…,100} wybieramy 51 liczb. Wykaż, że pewne dwie są względnie pierwsze (tj. nie mają wspólnego dzielnika pierwszego).
Zadanie VII
Ze zbioru {1,2,…,100} wybieramy 51 liczb. Wykaż, że jedna z nich jest podzielna przez drugą.
Zadanie VIII
Wykaż, że wśród dowolnych sześciu punktów w prostokącie 3×4 pewne dwa są odległe o nie więcej niż √5.
To już koniec naszego wpisu poświęconego Zasadzie szufladkowej Dirichleta. Mamy nadzieję, że jego lektura zachęciła Was do spróbowania własnych sił w Olimpiadzie Matematycznej! Żeby nauka była możliwie efektywna warto wesprzeć ją opieką laureatów najwyższych miejsc poprzednich edycji oraz profesjonalnie opracowanymi materiałami z teorią oraz selekcją zadań. Wszystko to znajdziecie w naszym kursie olimpijskim, który szczegółowo opisujemy na dedykowanej podstronie.

Strona przygotowana przez Zyskowni.pl