Miary asymetrii i kurtozy – kiedy dane są „krzywe”?

Statystyka opisowa to nie tylko średnia arytmetyczna i odchylenie standardowe. Gdy zagłębisz się w zagadnienie analizy danych, na pewno spotkasz też takie pojęcia miary asymetrii i kurtozy.

W tym artykule omówimy, czym są te miary, jak je interpretować oraz w jakich sytuacjach ich analiza jest szczególnie przydatna – również na Olimpiadzie Statystycznej. Jeśli chcesz jeszcze bardziej pogłębić temat, zachęcamy do sprawdzenia pełnej wersji kursu Indeksu w Kieszeni, gdzie pokazujemy, jak wykorzystać te wskaźniki w zadaniach olimpijskich.

www.pexels.com

Asymetria – czyli kiedy rozkład „przechyla się” na bok

Podręcznikowo asymetria (skośność) to miara opisująca symetrię rozkładu względem jego średniej. Co to oznacza w praktyce? Wyobraźmy sobie 3 zbiory danych:

A: {-2; 1; 1}

B: {-1; -1; 2}

C: {0; 0; 0}

Zauważ, że wszystkie 3 zbiory danych mają jednakową wartość średniej arytmetycznej (0) oraz zbiory A i B posiadają identyczną wartość odchylenia standardowego (2). Przeanalizujmy dokładniej te zbiory:

• Zbiór A posiada więcej liczb, które mają większe wartości od średniej arytmetycznej (posiada aż dwie „1”, jest to aż 2/3 elementów zbioru). Taki rozkład nazywamy lewostronnym (skośnym ujemnym), ponieważ jego współczynnik asymetrii jest ujemny¹ (-2/2, w przybliżeniu -0,707). Innym przykładem takiego zbioru może być wiek emerytów w ośrodku wypoczynkowym – większość ma ponad 65 lat, rzadko trafiają się osoby w wieku 55–60 lat, co lekko przechyla rozkład w lewo.

• Przeciwna sytuacja zachodzi w zbiorze B – posiada on więcej liczb, które mają mniejsze wartości (posiada aż dwie „-1”). Taki rozkład jest nazywany prawostronnym lub rozkładem skośnym dodatnim (wartość współczynnika asymetrii 2/2, w przybliżeniu 0,707). Inny przykład to rozkład zarobków w danym państwie – większość osób zarabia średnio lub mało, ale istnieje wąska grupa z bardzo wysokimi zarobkami. Zauważ, że współczynniki asymetrii zbiorów A i B znacznie się różnią mimo jednakowych wartości średniej arytmetycznej i odchylenia standardowego. To pokazuje, że klasyczne miary zróżnicowania, takie jak odchylenie standardowe, nie zawsze ujawniają różnice w kształcie rozkładu.

• Wreszcie zbiór C – wszystkie jego elementy mają jednakową wartość. Oznacza to, że rozkład ten jest idealnie symetryczny i w związku z tym wartość jego współczynnika asymetrii wynosi 0.  

Oto podsumowanie powyższych informacji w formie graficznej²:

Kurtoza – spiczaste czy płaskie?

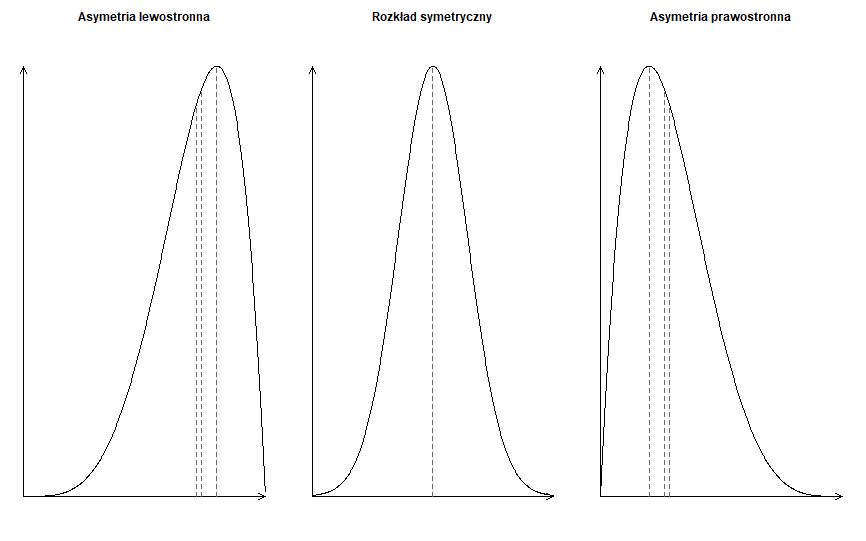
Kurtoza to skomplikowana miara, która opisuje kształt ,,szczytu’’ rozkładu. Jest to zagadnienie, które czasami pojawia się na późniejszych etapach Olimpiady. Należy jednak do zagadnień trudniejszych, dlatego tutaj omówimy je tylko pokrótce.  

Kurtoza mówi nam, jak bardzo dane skupiają się wokół średniej oraz jak wiele wartości skrajnych zawiera rozkład.

• Kurtoza dodatnia (leptokurtyczny rozkład) – rozkład ma wąski, wysoki szczyt i grube ogony. Oznacza to, że w najbliższym otoczeniu centrum rozkładu znajduje się najwięcej danych. Przykład: wyniki testu, gdzie większość uczniów uzyskała wynik bardzo zbliżony do średniego, ale rzadko pojawiają się skrajne przypadki (0% i 100%).
• Kurtoza ujemna (platokurtyczny rozkład) – rozkład bardziej „rozlany”, ma niższy szczyt i cieńsze ogony. Dane są rozproszone – znajdują się nie tylko w centrum, ale również w jego odległym sąsiedztwie. Przykład: liczba kroków dziennie wśród populacji – brak wyraźnej koncentracji wokół średniej.

Przykład praktyczny – analiza danych uczniów

Wyobraźmy sobie, że analizujemy liczbę godzin nauki uczniów przed Olimpiadą Statystyczną. Dane wyglądają następująco:

Średnia arytmetyczna to 7,25 godziny.

Mimo że większość uczniów uczyła się od 4 do 7 godzin, jeden z nich poświęcił aż 20 godzin, co może wpłynąć na asymetrię. Po obliczeniu współczynnika skośności otrzymujemy wartość dodatnią, co wskazuje na prawostronną asymetrię. Jest to zgodne z obserwacjami – zauważ, że zdecydowana większość wartości jest mniejsza niż średnia arytmetyczna. 

Kurtoza tych danych również okaże się dodatnia – większość uczniów poświęcała na naukę od 4 do 7 godzin, tylko 1 poświęcił na naukę aż 20h (tylko 1 wartość „daleko” od średniej arytmetycznej).

www.pexels.com

Dlaczego asymetria i kurtoza są ważne?

Na Olimpiadzie mogą pojawić się pytania zarówno obliczeniowe (np. oblicz współczynnik kurtozy/współczynnik asymetrii na podstawie danych, szczególnie na poprzednich etapach), jak i koncepcyjne (np. interpretacja wykresu lub wyniku, pytanie o wskazanie wykresu o asymetrii lewostronnej/prawostronnej itp.). 

Znajomość tych pojęć pomoże Ci lepiej zrozumieć dane oraz skuteczniej rozwiązywać zadania konkursowe. Jest to zagadnienie dość złożone, ale wiąże się z tym również fakt, iż stosunkowo niewielu uczestników Olimpiady ma je opanowane w stopniu wystarczającym. Znajomość miary asymetrii i kurtozy może dać Ci przewagę na Olimpiadzie Statystycznej – zwłaszcza tam, gdzie trzeba zrozumieć charakter danych, a nie tylko je przeliczyć.

To już wszystko w tym artykule! Chcesz więcej? Sprawdź ofertę naszego przygotowania do Olimpiad, gdzie przećwiczymy te zagadnienia na konkretnych przykładach zadań olimpijskich.

1.  W artykule obliczono tzw. klasyczny współczynnik asymetrii (ze względu na wykorzystanie miar takich jak średnia arytmetyczna i odchylenie standardowe). W polskiej literaturze istnieją również pozycyjny i mieszany współczynnik asymetrii, które są omawiane na naszym Kursie. 
   ↩︎
2.  Wykresy wykonano w języku programowania R. Pełna wersja na naszym Kursie.
   ↩︎