
Rachunek prawdopodobieństwa może wydawać się abstrakcyjny, dopóki nie zobaczymy, jak często wykorzystujemy go w praktyce: w statystyce medycznej, badaniach opinii, analizie ryzyka czy nawet w grach losowych. Jednym z najważniejszych narzędzi w tej dziedzinie – i jednym z najczęściej pojawiających się na maturze rozszerzonej z matematyki – jest Schemat Bernoulliego, znany także jako rozkład dwumianowy.
Najważniejsze informacje, których dowiesz się z tego artykułu:
Interesuje Cię matematyka? Koniecznie poznaj także podstawowe informacje o liczbie π!
Statystyka i rachunek prawdopodobieństwa to dla wielu uczniów jedne z najmniej lubianych działów matematyki. Choć pozornie oderwane od geometrii, funkcji czy algebry, w praktyce stanowią fundament nauk stosowanych: medycyny, ekonomii, psychologii czy inżynierii. To właśnie dzięki rachunkowi prawdopodobieństwa możemy ocenić ryzyko, przewidywać zjawiska lub badać procesy losowe.
W podstawie programowej na maturę rozszerzoną z matematyki od kilku lat znajduje się jedno z kluczowych zagadnień tej dziedziny – Schemat Bernoulliego (zwany również rozkładem dwumianowym). Pozwala on obliczyć prawdopodobieństwo uzyskania dokładnie k sukcesów w n niezależnych próbach, gdzie każda próba ma jedynie dwa możliwe wyniki: sukces lub porażkę.
Źródło: pixabay.com
Schemat Bernoulliego dotyczy serii n niezależnych prób, gdzie każda próba ma stałe prawdopodobieństwo sukcesu p i porażki 1−p. Aby obliczyć prawdopodobieństwo uzyskania dokładnie k sukcesów w tych n próbach, wykorzystuje się następujący wzór:
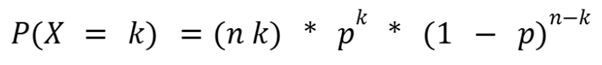
Schemat Bernoulliego wzór
Gdzie:

Bardzo ważne: każde zdarzenie jest niezależne od siebie i w każdym mamy taką samą szansę na sukces!
Schemat Bernoulliego opisuje sytuację, w której przeprowadzamy n niezależnych prób, a każda z nich ma:
Schemat Bernoulliego jest istotnym elementem podstawy programowej z matematyki na poziomie rozszerzonym, dlatego uczniowie przygotowujący się do matury muszą go dobrze opanować. Zagadnienie to w ostatnich latach dosyć często pojawia się w zadaniach dotyczących prawdopodobieństwa!
Wykonujemy 8 rzutów kostką. Oblicz prawdopodobieństwo, że dokładnie 3 razy wypadnie 6.
Dane:
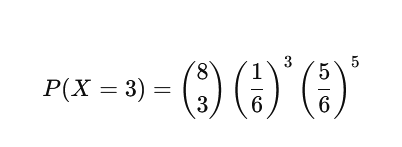
Prawdopodobieństwo, że podczas jednego testu czujnik wykryje błąd, wynosi p=0,1.
Oblicz prawdopodobieństwo, że w 6 próbach czujnik wykryje błąd przynajmniej raz.
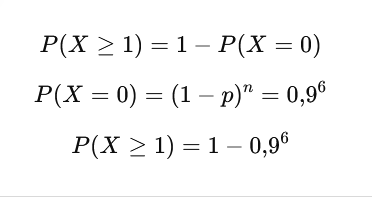
Wykonujemy 7 prób, każda z prawdopodobieństwem sukcesu p=0,6.
Oblicz prawdopodobieństwo, że sukcesów będzie więcej niż porażek.
Czyli szukamy:
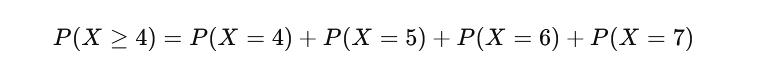
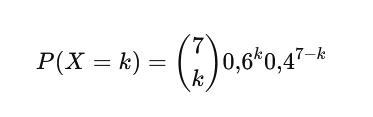
Schemat Bernoulliego to fundament rachunku prawdopodobieństwa – prosty w założeniach, ale niezwykle potężny w zastosowaniach. Pozwala modelować sytuacje, w których interesuje nas liczba sukcesów w określonej liczbie prób, a każda z nich ma tylko dwa możliwe wyniki. Choć idea może wydawać się teoretyczna, to właśnie na niej opiera się ogromna część współczesnych badań statystycznych:
Dzięki jednemu wzorowi możesz obliczyć prawdopodobieństwo dowolnej konfiguracji wyników – od wyrzucenia pięciu orłów w dziesięciu rzutach, po wykrycie błędu przez czujnik w serii testów. To właśnie ta uniwersalność sprawia, że schemat Bernoulliego regularnie pojawia się w zadaniach maturalnych: pozwala sprawdzić, czy uczeń nie tylko zna wzory, ale przede wszystkim rozumie zależności między nimi.
Dobrze opanowany schemat Bernoulliego to realna przewaga na egzaminie. Pomaga uporządkować myślenie o zadaniach z prawdopodobieństwa, skraca czas liczenia i pozwala uniknąć typowych błędów – jak mylenie liczby prób z liczbą sukcesów czy błędne traktowanie potęg pi 1-p. Połączenie teorii, przykładów i zadań z rozwiązaniami sprawia, że to zagadnienie staje się nie tylko zrozumiałe, ale wręcz intuicyjne.
W Indeksie w Kieszeni oferujemy kompleksowe kursy maturalne z matematyki – zarówno na poziomie podstawowym, jak i rozszerzonym! Sprawdź naszą ofertę i rozpocznij przygotowania, które pomogą Ci osiągnąć wymarzony wynik.
To model probabilistyczny opisujący liczbę sukcesów w serii niezależnych prób, gdzie każda próba ma stałe prawdopodobieństwo sukcesu p i dwa możliwe wyniki.
Gdy spełnione są trzy warunki:
Niczym – to dwie nazwy tego samego pojęcia.

Strona przygotowana przez Zyskowni.pl