
Siła dośrodkowa to jedno z tych pojęć fizycznych, które regularnie pojawia się na maturze i potrafi sprawić uczniom sporo trudności. Choć brzmi technicznie, opisuje zjawisko dobrze znane z codzienności – od ruchu samochodu na zakręcie po orbitowanie planet. W tym artykule wyjaśniamy, co musisz o niej wiedzieć, by zdobyć pewne punkty na egzaminie.
Najważniejsze informacje o sile dośrodkowej, których dowiesz się z tego artykułu:
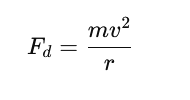
Interesujesz się fizyką i chcesz poznać również działanie zasady Fermata? Wszystko, co musisz o niej wiedzieć, znajdziesz w naszym drugim poradniku: https://indekswkieszeni.pl/zasada-fermata-jak-ja-zrozumiec-wszystko-co-musisz-wiedziec-na-olimpiadzie-fizycznej
Siła dośrodkowa to wypadkowa działająca tak, by zakrzywić tor ruchu i utrzymać ciało na okręgu. Zawsze jest prostopadła do prędkości i skierowana ku środkowi okręgu lub krzywizny. Jej rolę mogą pełnić różne rzeczywiste oddziaływania, na przykład grawitacja podtrzymująca satelitę na orbicie czy napięcie nici utrzymujące piłkę w ruchu po okrężnej trajektorii.
Przyjrzyjmy się prostej sytuacji. Zjawisko z ilustracji przedstawia pewną masę m przytwierdzoną do sznurka. Za jego pośrednictwem prostymi ruchami jesteśmy w stanie wprowadzić ją w ruch po okręgu. Innymi słowy: kręcimy sznurkiem z kulką. Dla uproszczenia załóżmy, że kulka porusza się ruchem jednostajnym, tzn. kulka kręci się ze stałą prędkością. Jak to możliwe, że utrzymuje się ona na swoim torze?
Aby to zrozumieć, musimy zejść poziom niżej – przyjrzyjmy się II zasadzie dynamiki Newtona: Jeżeli na dane ciało działa siła wypadkowa (różna od wektora zerowego), to ciało to porusza się ruchem zmiennym z przyspieszeniem wprost proporcjonalnym do tej siły i odwrotnie proporcjonalnym do masy ciała.
Inaczej mówiąc, jeżeli na danym kierunku występuje siła wypadkowa, która nie jest równa 0, to w danym kierunku mamy do czynienia z przyspieszeniem (zmianą prędkości w czasie). Jego wartość potrafimy obliczyć zgodnie ze wzorem:
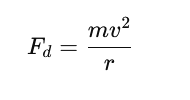
Następnie przyspieszenie generuje zmianę wartości lub/i kierunku wektora prędkości, a to generuje zmianę położenia.
Zaraz, zaraz! – ktoś może powiedzieć. Przecież w naszej sytuacji kulka porusza się jednostajnie. Prędkość się nie zmienia… FAŁSZ. Nie zmienia się wartość prędkości, ale zmienia się jej kierunek. Prędkość jest wektorem i jej zmiana może następować nie tylko poprzez wartość, ale także poprzez zwrot, kierunek i punkt przyłożenia. Zauważ, że podczas ruchu po okręgu kierunek prędkości nieustannie się zmienia. Oznacza to, że następuje zmiana tego wektora, a skoro tak, to ciało podlega przyspieszeniu. Skoro tak, to zgodnie z II zasadą dynamiki Newtona w układzie występuje siła wypadkowa, która doprowadza do tej zmiany.
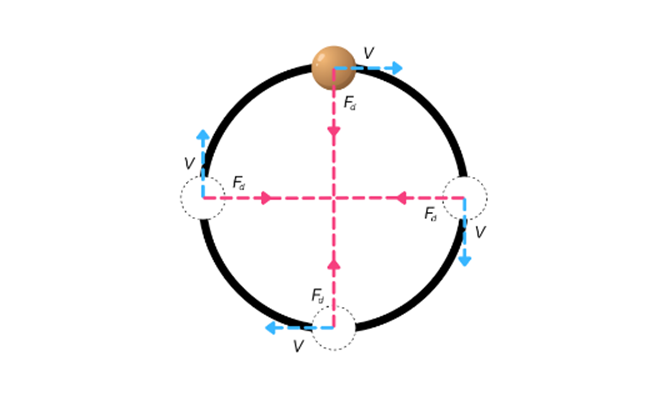
Siłą, która utrzymuje ruch po okręgu, jest siła napięcia sznurka – to ona powoduje, że nasze ciało porusza się po okręgu. Napięcie sznurka w układzie inercjalnym (gdy patrzymy z boku) odpowiada właśnie za ruch tego ciała po okręgu. To właśnie siłę napięcia sznurka możemy nazwać siłą dośrodkową.
Generalizując, to siła dośrodkowa wymusza na układzie ruch po okręgu – zmianę kierunku wektora prędkości. Zauważ, że po puszczeniu sznurka masa poruszać się będzie ruchem prostoliniowym po torze stycznym do okręgu i o kierunku zgodnym z chwilowym kierunkiem prędkości. Mówiąc prościej: zniknęła siła, która generowała zmianę kierunku prędkości. Skoro siła wypadkowa jest już zerowa, to nie ma przyspieszenia, a więc prędkość pozostaje stała. Stała pozostaje wartość, ale także kierunek, zwrot i punkt przyłożenia. Ten ostatni fakt wynika z I zasady dynamiki Newtona: ciało, na które nie działa żadna siła (siła wypadkowa równa 0), porusza się ruchem jednostajnym prostoliniowym lub nie porusza się wcale.
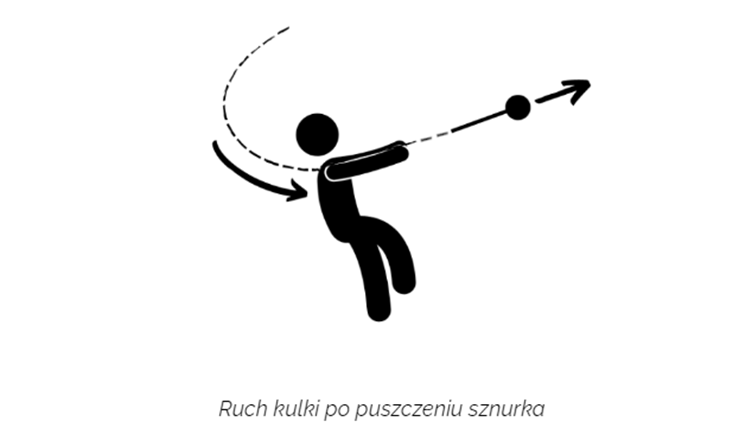
Pragnę podkreślić, bo pewnie przegapiłeś drogi czytelniku ten fakt, że nie istnieje coś takiego jak siła dośrodkowa. Nie ma takiej siły samej w sobie. Prawdą jest za to, że pewne siły mogą pełnić funkcję siły dośrodkowej. Na przykła. w ruchu satelity wokół Ziemi siła grawitacji pełni funkcję siły dośrodkowej. W przypadku samochodu znajdującego na zakręcie jest to siła tarcia. Dla elektronu krążącego wokół jądra atomowego – siła Coulomba, a w przypadku kulki na sznurku siła naciągu nici. W efekcie często w zadaniach przyrównujesz je do siebie, ale teraz wiesz już, dlaczego jest to dozwolone!
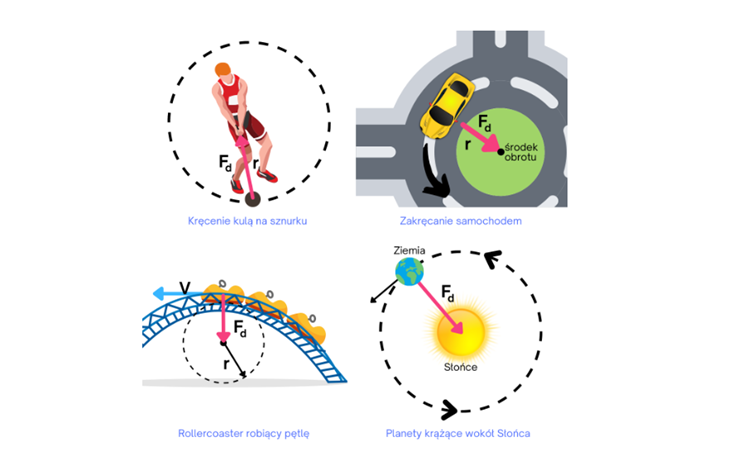
To są przykłady z pojedynczymi siłami – co jednak w sytuacji, gdy na dane ciało oddziałuje wiele sił? Która jest dośrodkową? Jest to przypadek ogólniejszy! W praktyce to siła wypadkowa w kierunku promienia (w kierunku radialnym) pełni funkcję siły dośrodkowej. Zatem trzeba zobaczyć, jaka jest siła wypadkowa na tym kierunku, i przyrównać ją do siły dośrodkowej.
Skoro już czujemy, czym jest siła dośrodkowa, tzn. wiemy, że pewne siły mogą pełnić jej funkcję, to od czego zależy jej wartość? Wyjaśnijmy:
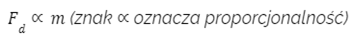
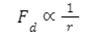
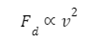
Podsumowując: jeżeli chcemy kręcić ciałem o masie m, które będzie poruszać się z prędkością v, po okręgu o promieniu l, to musi zadziałać siła równa co do wartości:
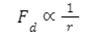
Zacznijmy od tego, że masa we wzorze na siłę dośrodkową jest masą ciała, które podlega przyspieszeniu. Jest to dokładnie to ciało, które porusza się po okręgu. W przypadku naszej sytuacji jest to po prostu kulka. Jednakże, jeżeli mamy kilka obiektów w obrębie jednego ciała, np. samochód poruszający się na zakręcie, to ciałem jest nie tylko samochód ms, ale także pasażerowie mp wewnątrz pojazdu. Oznacza to, że ciałem jest cała masa, której tor zakrzywia się. Napisalibyśmy wtedy m=ms+mp.
We wzorze na Fd promieniem r jest promień faktycznego okręgu, po jakim porusza się ciało. Zatem zawsze musimy zidentyfikować, gdzie jest środek tego okręgu! Zobacz, że na poniższej sytuacji osoba stojąca na Ziemi o promieniu RZ, na pewnej szerokości geograficznej porusza się po okręgu nie o promieniu R= RZ, a o promieniu:
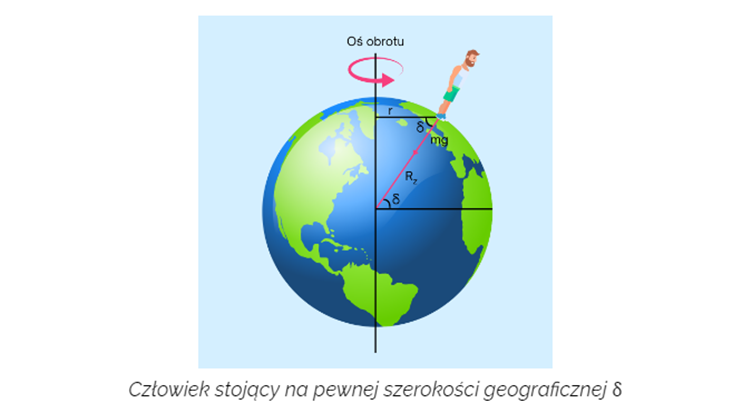
Ciało może poruszać się po okręgu również w innych sytuacjach. Samochód na górce lub w dołku, karuzela na placu zabaw, krążące planety – to jedne z nich. Wszędzie tam, gdzie ciało porusza się po okręgu, musi istnieć wypadkowa siła w kierunku promienia (w kierunku radialnym). Pełni ona funkcję siły dośrodkowej!
Promień nie musi być stały. W przypadku ruchu po okręgu promień ma zawsze stałą wartość. Jednak np. w przypadku ruchu po elipsie już tak nie jest (promień ulega ciągłej modyfikacji pod względem długości).
Na koniec została prędkość, której wartość zawsze określamy odnosząc się do promienia toru ruchu naszego ciała. O co chodzi? Prędkość w ruchu krzywoliniowym (w tym po okręgu) jest prostopadła do chwilowego promienia. Najłatwiej zrozumieć to na poniższym przykładzie.
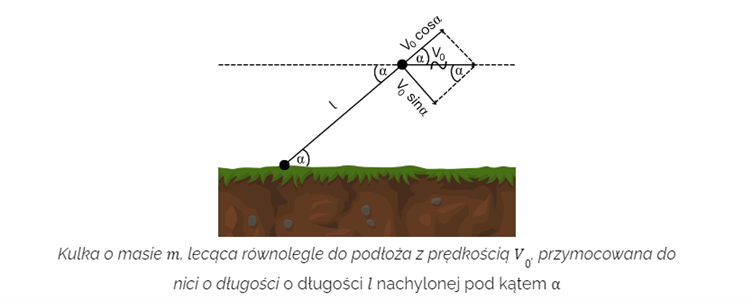
Kulka o masie m leci równolegle do podłoża z prędkością V0 i została złapana przez nić o długości l nachyloną pod kątem α do tego podłoża. Ile wynosi siła dośrodkowa po ustabilizowaniu ruchu?
Otóż należy rozłożyć wektor prędkości na dwie składowe: równoległą do nici Vr= V0 cos α i prostopadłą do tej nici Vt= V0 sin sin α. Składowa równoległa zostanie wytracona przy założeniu, że nić jest nierozciągliwa, nie zerwie się itd. Będzie to się wiązało z powstaniem chwilowej, zwiększonej siły hamującej. Musi ona zmniejszyć prędkość równoległą do zera (patrz pędowa postać zasady dynamiki Newtona). Z kolei składowa prostopadła odpowiadałaby już za docelowy ruch kulki po okręgu i wchodziła w skład naszego wzoru na siłę dośrodkową po ustabilizowaniu:
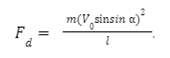
Na końcu warto wspomnieć, że oczywiście prędkość też nie musi być stała. Może ulegać ciągłej zmianie na skutek działania siły stycznej na ciało. Wtedy wypadkowa siła styczna odpowiada za przyspieszenie styczne, a to za zmianę wartości prędkości. Z kolei wypadkowa siła radialna odpowiada za przyspieszenie dośrodkowe, a to za zmianę kierunku prędkości.
Samochód o masie 1200 kg porusza się po łuku drogi o promieniu 50 m z prędkością 54 km/h. Oblicz wartość siły dośrodkowej działającej na pojazd. Wynik podaj w niutonach.
Wzór na siłę dośrodkową
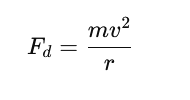
Podstawienie danych

Odpowiedź: Siła dośrodkowa działająca na samochód wynosi 5400 N.
Kulka o masie 0,5 kg jest obracana po poziomym okręgu na sznurku o długości 0,8 m. Jej prędkość wynosi 4 m/s. Oblicz wartość siły dośrodkowej, która działa na kulkę.
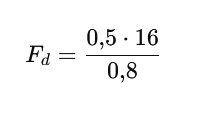
Siła dośrodkowa działająca na kulkę wynosi 10″ N” .
Na koniec chciałbym, abyś zapamiętał drogi czytelniku, jeszcze jeden fakt. Siła dośrodkowa i odśrodkowa to dwie różne rzeczy i nigdy nie mogą wystąpić na jednym rysunku! Na dobrą sprawę w układzie inercjalnym (obserwator z boku) na rysunku nie narysujemy siły dośrodkowej. To inne siły, jak już wiesz, pełnią jej funkcję. W przypadku siły odśrodkowej powinna się ona znaleźć na rysunku. Uzyskujemy wtedy zupełnie inną interpretację fizyczną – przechodzimy do układu nieinercjalnego, ale o tym już innym razem!
Chcesz dobrze przygotować się do egzaminu z fizyki? Jeżeli tak, to zachęcamy do zapoznania się z naszą ofertą kursów maturalnych z fizyki!
Siła dośrodkowa to siła, która umożliwia ruch po okręgu. Jej kierunek jest zawsze skierowany do środka okręgu, a jej działanie powoduje zmianę kierunku ruchu, a nie jego prędkości. Siła dośrodkowa nie jest osobnym typem siły – jej rolę może pełnić np. tarcie, napięcie nici czy grawitacja.
Siła dośrodkowa rośnie, gdy zwiększamy masę ciała lub prędkość (działa tu zależność kwadratowa – podwojenie prędkości zwiększa siłę czterokrotnie), natomiast maleje, gdy zwiększamy promień toru ruchu.
Nie. Ponieważ siła dośrodkowa działa prostopadle do prędkości, nie może zmieniać energii kinetycznej ciała – powoduje jedynie zmianę kierunku ruchu.
Tak – ale nie jest to nowy rodzaj siły. To nazwa funkcji, jaką pełni jedna z sił działających na ciało. W różnych sytuacjach siłą dośrodkową może być:

Strona przygotowana przez Zyskowni.pl