Z pewnością każdy ósmoklasista w swojej karierze matematycznej spotkał się z wyzwaniem polegającym na obliczeniu prędkości pojazdu, gęstości substancji czy objętości bryły. Czasami takie zadania stanowią nie lada wyzwanie, dlatego w tym poście zdradzimy parę sztuczek, które mogą ułatwić podanie prawidłowej odpowiedzi na egzaminie ósmoklasisty z matematyki!
Metoda ta świetnie się sprawdza przy obliczaniu gęstości lub prędkości oraz ich składowych.
Wzór na gęstość (d) ma postać: d = m/V, gdzie m oznacza masę, a V objętość. Używając trójkąta, zapisalibyśmy to w następującej postaci:
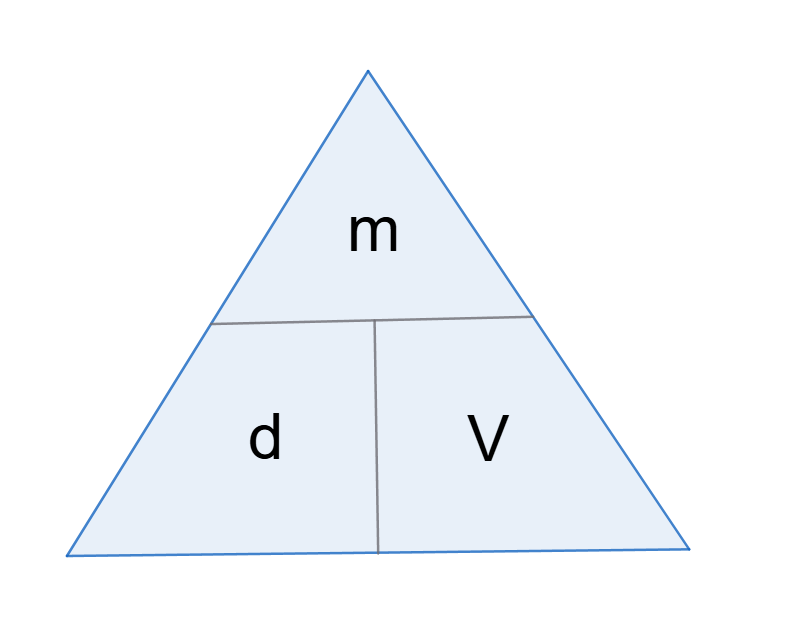
Zauważ, że skoro m jest w liczniku ułamka, to jest zapisany wyżej niż pozostałe parametry.
Zasady są proste:
1. Zasłaniamy parametr, który chcemy wyliczyć.
2. Pozostałe parametry zapisujemy po drugiej stronie równania, z zachowaniem poziomów obecnych w trójkącie:
Przykład:
Gdybyśmy chcieli wyliczyć masę na podstawie podanej objętości i gęstości, to wystarczy, że zasłonimy w tym trójkącie masę. Zostanie nam wtedy d i V na tym samym poziomie trójkąta:
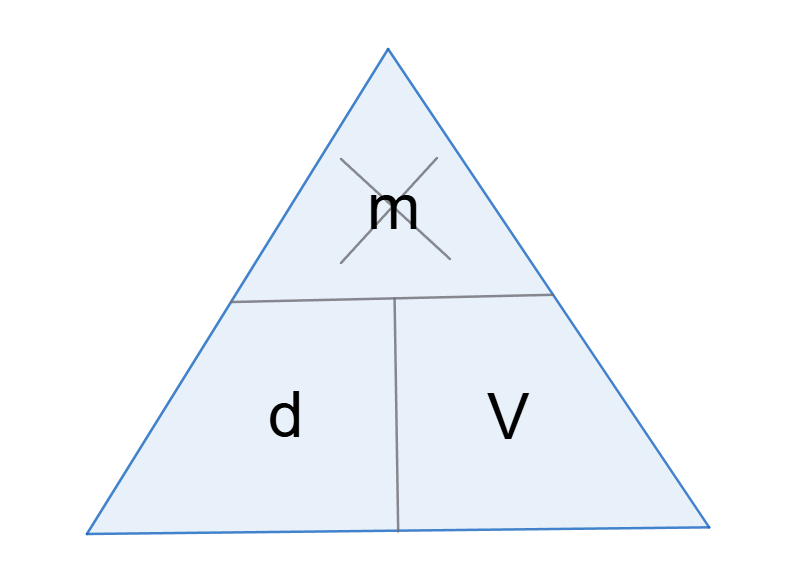
Co oznacza, że wzór na masę to m = d*V
Uwaga! Bardzo istotne jest oczywiście zachowanie zgodnych jednostek, co oznacza, że jeśli podana jednostka gęstości to g/cm3 , to zależy nam na tym, żeby masa była w gramach i objętość w cm3 !
Analogicznie możemy postąpić ze wzorem na prędkość: V = s/t, gdzie:
Możemy przedstawić ten wzór za pomocą trójkąta:
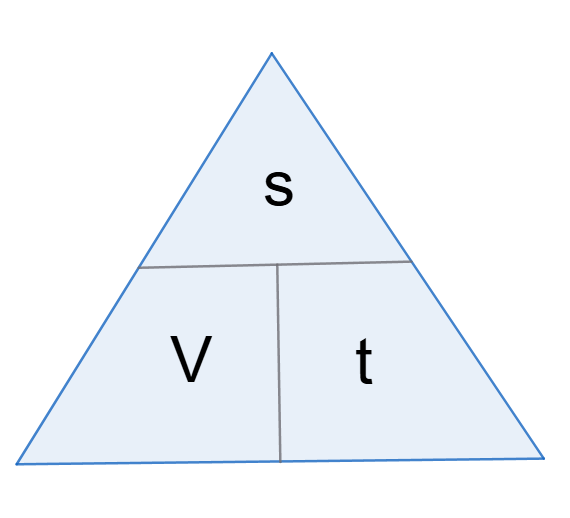
W tym momencie spróbujcie samodzielnie wyznaczyć wzór na czas, korzystając z trójkąta.
Jest to bardzo przydatny manewr, który pomaga wyznaczyć wzór skomplikowanych parametrów, takich jak wcześniej wspomniane gęstość i prędkość, patrząc jedynie na rozlokowanie jednostek.
Przykład:
Wiemy, że typową jednostką prędkości są km/h. Kilometry są jednostką drogi (s), natomiast h, czyli godziny, są jednostką czasu (t), zatem skoro dzielimy kilometry przez godziny, to w takim razie, żeby otrzymać wzór na prędkość, musimy podzielić drogę przez czas, zatem:
V = s/t
No dobrze, jak jesteśmy w temacie jednostki km/h, to przypomnijmy sobie, w jaki sposób możemy sprawnie przekształcić km/h na m/s.
1km = 1000 m
1 h = 60 min = 60*60 s = 3600 s
km/h = 1000m/60min = 1000m/(60*60 s) = 1000/3600*m/s = 10/36 m/s
Zatem:
1 m/s = 3,6 km/h
co oznacza, że:
25 m/s = 3,6 * 25 km/h = 90 km/h
Tutaj znowu najprościej posłużyć się jednostkami danych parametrów.
Jak już dobrze wiemy, jednostką pola są np. cm2 , natomiast objętości cm3. Analogiczne wykładniki potęg, które zastosujemy we wzorach mają postać:
Pamiętajcie, że najważniejszą zasadą jest zachowanie prawidłowych jednostek, aby sprawnie poruszać się między poszczególnymi parametrami. Trzymamy za Was kciuki na egzaminie ósmoklasisty, powodzenia!
Nie zwlekaj — dołącz do naszych kursów i rozpocznij kompleksowe przygotowanie do egzaminu ósmoklasisty z Indeksem w Kieszeni!
Strona przygotowana przez Zyskowni.pl
Zakładamy Ci konto na naszej platformie e-learningowej, na której znajdują się materiały, artykuły popularnonaukowe, czy nagrania video! Możesz tam bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane do sprawdzenia prace.
Na platformie otrzymujesz moduły - zestawy materiałów z prezentacjami, skryptami, testami, kartkówkami. Z nimi pracujesz w dowolnym miejscu - w domu, w podróży, w bibliotece.
Na platformie, gdzie odbywa się kurs możesz zadawać pytania 24h na dobę 7 dni w tygodniu - Prowadzący są tam po to by zawsze Ci pomóc i rozwiać Twoje wątpliwości.
Twój progres w nauce jest kontrolowany wraz z każdym kolejnym modułem - służą temu wszelkie kartkówki, testy i sprawdziany, które rozwiązane odsyłasz i otrzymujesz szczegółowy klucz.
Celujesz w świetny wynik na egzaminie ósmoklasisty? A może potrzebujesz tylko usystematyzować posiadaną wiedzę? Nieważne - nasz kurs (tempo pracy i materiały oraz pomoc Prowadzącego) jest zawsze dopasowany do aktualnego stanu Twoich umiejętności i oczekiwań.
Na platformie otrzymasz nielimitowany w okresie przygotowań dostęp do nagrań video, na których nasz zespół merytoryczny przeprowadzi Cię przez najbardziej wymagające i najczęściej pojawiające się na arkuszu zagadnienia egzaminacyjne.
Indywidualny kurs e-learningowy
egzamin ósmoklasisty
Wolisz uczyć się we własnym tempie i na własnych zasadach? W takim razie kurs e-learningowy jest stworzony właśnie dla Ciebie!
Nowoczesna forma indywidualnej nauki zdalnej (start: natychmiast lub we wskazanym terminie)
Dostęp do dedykowanej platformy do nauki e-learningowej
Harmonogram przygotowań dostosowany do dostępności ucznia
Przypisany opiekun merytoryczny prowadzący kurs
Komplet materiałów podzielonych na moduły tematyczne, a w każdym z nich: prezentacje, testy, kartkówki, skrypty, karty pracy i zadania egzaminacyjne
Materiały video – do kursu dołączone są nagrania video, na których członkowie zespołu merytorycznego IWK tłumaczą najtrudniejsze lub najbardziej prawdopodobne w wystąpieniu na egzaminie zagadnienia
Indywidualne podejście – otrzymujesz dostęp do naszej dedykowanej platformy edukacyjnej z pomocami naukowymi, na której możesz bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane prace.
Regularnie sprawdzane postępy
Ciągła możliwość kontaktu z Prowadzącym
Dzięki nowoczesnej formie nauki nasze kursy są dostępne dla uczniów z całej Polski – możesz dołączyć do nich niezależnie od miejsca zamieszkania i zacząć przygotowania już dziś! Skontaktuj się z nami i nie odkładaj decyzji na później – do egzaminu ósmoklasisty coraz bliżej!
Grupowy kurs całoroczny
egzamin ósmoklasisty
Chcesz solidnie przygotować się do egzaminu ósmoklasisty? Wolisz regularne zajęcia w grupie i stałe wsparcie prowadzącego? Jeśli tak, kurs grupowy będzie idealnym wyborem dla Ciebie!
46 godzin lekcyjnych zajęć (23 spotkania) + prace domowe
Forma stacjonarna (w salach w Warszawie) lub webinarowa (zajęcia online na żywo)
Nagrania z zajęć webinarowych oraz nagrania umożliwiające nadrobienie materiału osobom zapisującym się po rozpoczęciu kursów stacjonarnych
Możliwość wyboru grupy zajęciowej (harmonogram pojawi się w lipcu 2026 r.)
Pomoc pomiędzy zajęciami – ciągła możliwość kontaktu z Prowadzącym przez dedykowaną grupę zajęciową
Materiały z zajęć w formie cyfrowej
Regularne zajęcia pomagają utrzymać systematyczność w nauce i realnie wpływają na lepsze wyniki na egzaminie ósmoklasisty. Co roku wielu naszych uczniów z różnych części Polski osiąga wysokie rezultaty. Zapisz się na zajęcia już dziś i przygotuj się z nami do egzaminu ósmoklasisty!