
Liczba π (pi) to jedna z najbardziej rozpoznawalnych i fascynujących stałych w historii matematyki. Symbolizuje stosunek obwodu koła do jego średnicy – prosty, a zarazem genialny związek, który pojawia się nie tylko w geometrii, ale również w fizyce, analizie matematycznej, informatyce i statystyce. Od czasów starożytnych π rozpala wyobraźnię uczonych – od Babilonu i Egiptu po współczesne laboratoria obliczeniowe. Jej rozwinięcie dziesiętne jest nieskończone i nieokresowe, co oznacza, że liczba π należy do liczb niewymiernych.
Najważniejsze informacje o liczbie π, których dowiesz się z tego artykułu:
Przygotowujesz się do egzaminu dojrzałości? Sprawdź, co musisz wiedzieć o optymalizacji na maturze z matematyki
Liczba π (pi) to jedna z najważniejszych stałych matematycznych, definiowana jako stosunek obwodu koła do jego średnicy, czyli π = C/d. To niezwykle uniwersalna liczba, pojawiająca się w dziesiątkach dziedzin nauki – od geometrii i trygonometrii, przez analizę matematyczną i fizykę, aż po statystykę i informatykę. To sprawia, że liczba π jest jedną z kluczowych stałych matematyki.
W praktyce używamy przybliżenia π ≈ 3,14159…, często skracanego do 3,14, jednak ta pozornie prosta liczba skrywa ogromną głębię – od fascynującej historii po niezwykłe ciekawostki, które do dziś inspirują matematyków i miłośników nauki na całym świecie.
Data obchodów Dnia Liczby π (Pi Day) nie jest przypadkowa. W amerykańskim formacie zapisu dat (miesiąc/dzień) 14 marca zapisuje się jako 3.14, co odpowiada pierwszym cyfrom rozwinięcia dziesiętnego liczby π.
Jeśli ktoś przegapi marcowe święto, może uczcić Dzień Aproksymacji Pi, przypadający 22 lipca (22/7 ≈ 3.14) – to popularne historyczne przybliżenie π.

Źródło: www.pixabay.com
Najbardziej znaną w skali świata stałą matematyczną najprościej opisać korzystając ze wzoru, który dzieci poznają już w podstawówce (pamiętacie, obwód koła = 2πr). Definicja jest następująca: w geometrii euklidesowej (klasycznej) π jest równe stosunkowi długości obwodu okręgu do długości jego średnicy. Tę zależność zauważono już w Babilonii ponad 4000 lat temu, ale niektórzy badacze sądzą, że była ona znana i stosowana już w starożytnym Egipcie, ponad 1000 lat wcześniej. Okazuje się, że stosunek obwodu piramidy Cheopsa do jej wysokości wynosi 921 m/147 m ≈ 6,28 = 2π. Część egiptologów uważa, że nie może to być dziełem przypadku.
Liczbę π można też określić jako pole koła o promieniu równym 1 (kolejny wzór do przypomnienia: pole koła = πr2). Wspinając się o parę stopni zaawansowania wyżej, do zdefiniowania tej liczby użyjemy funkcji trygonometrycznych: π to najmniejsza dodatnia liczba x, dla której sin(x) = 0. Mnogość możliwych charakterystyk jest zasługą szerokiego zastosowania π w różnych wzorach, od geometrii analitycznej i probabilistyki (rachunek prawdopodobieństwa) po fizykę kwantową i elektrostatykę.
Liczbę π można również opisać na różne sposoby:
Mnogość sposobów definiowania π wynika z jej ogromnego znaczenia i wszechobecności w świecie nauki.
Każdy uczeń wie, a przynajmniej powinien wiedzieć, że π ≈ 3,14. Ktoś bardziej dociekliwy przypomni sobie dwa kolejne rozwinięcia dziesiętne i uzyska π ≈ 3,1415. Nadal nie jest to dokładne określenie jej wartości. Ta sztuka nigdy się nie uda z prostej przyczyny: liczba π jest liczbą niewymierną, co udowodnił w 1761 roku Johann Heinrich Lambert. To, że π jest niewymierna, oznacza mniej więcej tyle, że… nie jest wymierna, czyli nie da się jej zapisać w postaci ilorazu dwóch liczb p i q, gdzie p i q są całkowite i q jest różne od zera.
Mówiąc prościej: rozwinięcie dziesiętne liczby π jest nieskończone i nieokresowe. Mówiąc jeszcze prościej: kolejne cyfry rozwinięcia dziesiętnego liczby π są „ustawione” w kompletnie nieuporządkowany sposób. To właśnie czyni z niej jedną z najbardziej tajemniczych i intrygujących liczb w całej matematyce.
Każdy zna przybliżenie π ≈ 3,14, ale jej rozwinięcie dziesiętne jest nieskończone i nieokresowe:
π = 3, 3,14159265358979323846264338327950288419716939937510
Dzięki współczesnym superkomputerom znamy dziś wartość liczby π z dokładnością do bilionów cyfr po przecinku. W praktyce jednak do większości obliczeń wystarcza zaledwie kilka miejsc dziesiętnych – na przykład:
Ta nieskończona precyzja ma znaczenie głównie symboliczne – matematyka zna liczbę π dokładnie, choć człowiek nigdy nie zapisze jej w całości.

Źródło: www.pixabay.com
Współczesne superkomputery potrafią obliczyć wartość liczby π z niewyobrażalną dokładnością. Do niedawna rekord wynosił 22,5 biliona miejsc po przecinku, a obliczenia zajęły 105 dni pracy maszyny i około 120 terabajtów pamięci dyskowej. Dziś, dzięki postępowi technologicznemu, znamy już ponad 300 bilionów cyfr liczby π (rekord z 2025 roku – KIOXIA & Linus Media Group). To rozwinięcie jest w praktyce tak nieskończenie długim łańcuchem cyfr, że można w nim znaleźć każdą liczbę naturalną, jaka tylko przyjdzie do głowy.
Dla przykładu:
Według analiz prawdopodobieństwa:
Takie właściwości rozwinięcia liczby π są jednym z powodów, dla których uchodzi ona za nieskończoną i chaotyczną w swojej strukturze, mimo że jest precyzyjnie zdefiniowaną matematyczną stałą.
Niewymierność π nie jest jedynym problemem, który spędza sen z oczu matematykom. W 1882 roku Ferdinand Lindemann udowodnił, że jest ona również liczbą przestępną (na marginesie: liczby, które nie są przestępne, to liczby algebraiczne). Oznacza to, że nie istnieje wielomian o współczynnikach wymiernych i niezerowych W(x) taki, że W(π) = 0 (czyli przyjmuje dla liczby wartość równą zero).
Na marginesie: zerowym jest wielomian, który dla dowolnej liczby rzeczywistej x przyjmuje wartość równą zero; z definicji wielomian niezerowy to… taki wielomian, który nie jest wielomianem zerowym. Liczb przestępnych znamy mało. Należy do nich m.in. liczba Eulera (e ≈ 2,71), kolejna, obok liczby π, bardzo ważna stała matematyczna.
Najwcześniejsze teksty świadczące o świadomych śladach użycia π pochodzą z ok. 1900 r. przed Chrystusem. W egipskim Papirusie Matematycznym Rhinda, który zawiera 87 zadań z komentarzem (jest to najprawdopodobniej najstarszy zbiór zadań na świecie) figuruje pod postacią 256/81 ≈ 3,16, a w babilońskich tabliczkach datowanych na ten sam okres jako 25/8 ≈ 3,125. W starożytności badano ją też po drugiej stronie globu: w Indiach i Chinach. Zu Chongzhi, nadworny astrolog chińskiego cesarza, określił π jako 355/113 ≈ 3,14159 – było to najdokładniejsze przybliżenie aż do XV wieku.
Nasza bohaterka pojawia się również w Starym Testamencie, w Drugiej Księdze Kronik w opisie ceremonialnego basenu króla Salomona: Następnie sporządził odlew okrągłego „morza” o średnicy dziesięciu łokci, o wysokości pięciu łokci i o obwodzie trzydziestu łokci. Jak widać twórca tego „morza” przyjął π = 3.
Dopiero Archimedes był pierwszym matematykiem, który zajął się liczbą π na poważnie i badał jej dokładną wartość. Udało mu się ją oszacować z dokładnością do drugiego miejsca po przecinku korzystając z różnych zależności geometrycznych. Grecki matematyk wyznaczył długości boków dwóch 96-kątów foremnych, czyli takich figur, które mają boki o równej długości: opisanego na okręgu i wpisanego w ten sam okrąg, a następnie obliczył średnią arytmetyczną obwodów tych wielokątów. W ten sposób otrzymał przybliżoną wartość obwodu podanego okręgu.
Archimedes obliczył, że π należy do przedziału (3 ; 3 ). Przeprowadzone obliczenia były jednak bardzo żmudne i czasochłonne. Mimo wielkich wysiłków Archimedesowi nie udało się dokonać analogicznych obliczeń dla 192-kątów, co pozwoliłoby mu wyznaczyć π z jeszcze większą dokładnością. W późniejszych stuleciach uważano jego metodę za najlepszą i często ją wykorzystywano.
W 1400 roku hinduski matematyk Madhava wymyślił nowy sposób: jako pierwszy w historii do obliczenia wartości π użył ciągów nieskończonych. W istocie odkrył on wzór, do którego Gottfried Wilhelm Leibniz i James Gregory doszli niezależnie od siebie ponad 300 lat później. Wzór Madhavy-Leibniza lub Leibniza-Gregory’ego wygląda następująco:
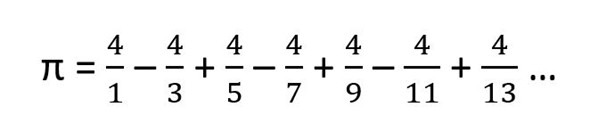
Takie postępowanie przyjęło się i od tego czasu zaczęto używać ciągów nieskończonych. Mimo tej innowacji w 1596 roku Ludolph van Ceulen podał przybliżenie π z dokładnością do 35. miejsca po przecinku używając metody Archimedesa. Skorzystał z wieloboku o… 262 bokach! Nic dziwnego, że swoje obliczenia prowadził przez całe życie, a liczbę π zaczęto czasami nazywać od jego imienia ludolfiną. Określona przez niego wartość została nawet wyryta na jego płycie nagrobkowej.
Z biegiem lat uzyskiwano coraz lepsze przybliżenia sięgające kilkuset miejsc po przecinku. W 1853 William Rutherford doszedł do 440. miejsca, a rekordzistą w ręcznych obliczeniach jest William Shanks, któremu w 1874 udało się ustalić 707. miejsce. Zajęło mu to ponad 15 lat (niestety okazało się, że popełnił błąd w obliczeniach i 180 ostatnich cyfr jest nieprawidłowych). W XX wieku zaczęto używać komputerów i obecnie stosuje się wyłącznie takie metody.

Źródło: www.pixabay.com
Starożytni Grecy sformułowali zasady konstrukcji figur przy pomocy jedynie linijki i cyrkla. Te narzędzia są w założeniu wyidealizowane: cyrkiel może być rozwarty na dowolną szerokość, a linijka ma potencjalnie nieskończoną długość. Takie rodzaje konstrukcji noszą miano klasycznych. Jak można się domyślić, ta metoda nie jest doskonała.
Grecy przez wieki próbowali rozwiązać trzy słynne zagadnienia, które spędzały sen z powiek największym umysłom tamtej epoki:
Żadnego z tych problemów nie da się rozwiązać metodami klasycznymi, czyli przy pomocy samej linijki i cyrkla.
Otóż jej przestępność ostatecznie rozstrzyga ostatni problem. Współrzędne wszystkich punktów, które można skonstruować za pomocą konstrukcji klasycznej są liczbami algebraicznymi, czyli (jak pokazano wcześniej) takimi, które nie są przestępne. A π do nich nie należy.
To pokazuje, że kwadratura koła jest niewykonalna. Udowodnił to dopiero Pierre Wantzel w 1837 roku. Mimo tego istnieje sposób na wyznaczenie odcinka o długości zbliżonej do wartości liczby π.
Choć idealna kwadratura koła jest niemożliwa, Polak – Adam Adamandy Kochański, nadworny matematyk króla Jana III Sobieskiego, w 1685 roku opracował konstrukcję przybliżoną. Pozwala ona geometrycznie wyznaczyć odcinek o długości bardzo zbliżonej do wartości pi, z błędem mniejszym niż 0,002%!
To rozwiązanie, znane dziś jako konstrukcja Kochańskiego, do dziś budzi podziw swoją elegancją i prostotą.
Może ciężko w to uwierzyć zwykłym zjadaczom chleba, ale π ma swoich licznych i zagorzałych wielbicieli. Powstało nawet pojęcie pifilologia (z ang. piphilology), które oznacza tworzenie i posługiwanie się technikami pozwalającymi na zapamiętanie jak najdłuższego ciągu cyfr rozwinięcia dziesiętnego π. Rekord ustanowił Akira Haraguchi, który zapamiętał równo 100 tysięcy cyfr w poprawnej kolejności!
Do pomocy w zapamiętywaniu można używać specjalnych wierszy i opowiadań, w których długość każdego kolejnego słowa jest równa kolejnej cyfrze w rozwinięciu dziesiętnym. Ten styl pisania nosi nazwę pilish, a te krótkie utwory są znane w języku angielskim jako piems (połączenie słów pi i poems). Najsłynniejszy utwór został stworzony przez sir Jamesa Jeansa. Brzmi on następująco: How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics! (w tłumaczeniu: Jakże chciałbym się napić, czegoś mocniejszego oczywiście, po trudnych wykładach dotyczących mechaniki kwantowej!). Istnieje też kilka przykładów w języku polskim. Oto jeden z nich:
Jaś o kole z werwą dyskutuje
bo dobrze temat ten czuje
zastąpił ludolfinę słowami wierszyka
czy Ty już odgadłeś, skąd zmiana ta wynika?
Oto i wiem i pomnę doskonale…
Kto z woli i myśli zapragnie Pi spisać cyfry, ten zdoła.
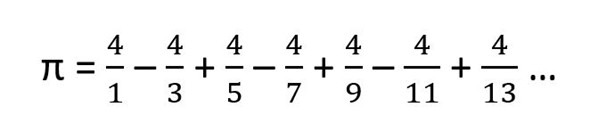
Liczba π (pi) to nie tylko matematyka, ale też inspiracja, święto i kulturowy fenomen. Oto kilka z najciekawszych faktów, które warto znać!
Liczba pi ciekawostki:
Liczba π to jedna z najważniejszych stałych matematycznych – uniwersalna, fascynująca i obecna w niezliczonych dziedzinach nauki. Choć znamy ją od starożytności, do dziś pozostaje źródłem inspiracji, a jej nieskończone rozwinięcie pokazuje, jak wiele tajemnic wciąż kryje matematyka. Dzięki swojej prostocie i jednocześnie niezwykłej złożoności π na zawsze pozostanie symbolem ciekawości i nieustannego dążenia człowieka do poznania świata.
Liczba pi to podstawowa wiedza z matematyki, która przyda Ci się na:
To stała matematyczna równa stosunkowi obwodu koła do jego średnicy (π = C/d).
W przybliżeniu 3,14159… – rozwinięcie jest nieskończone i nieokresowe.
Nie da się jej zapisać jako ułamek p/q. Jej rozwinięcie dziesiętne nie powtarza się i nie kończy.
Nie jest pierwiastkiem żadnego wielomianu o współczynnikach wymiernych; to dowód, że kwadratura koła jest niemożliwa.
W geometrii (koła, kule), trygonometrii, fizyce, inżynierii, statystyce i informatyce.

Strona przygotowana przez Zyskowni.pl