Od 2015 roku na maturze rozszerzonej z matematyki pojawiły się zadania z wykorzystaniem pochodnej. Najważniejszym z nich jest zadanie optymalizacyjne, za które można zdobyć od 5 do 7 punktów, co daje między 10% a 14% możliwych do zdobycia punktów.
Zadania optymalizacyjne dotyczą najczęściej zagadnień związanych z działami takimi jak: planimetria, trygonometria, stereometria, geometria analityczna. Jak je rozwiązać?
Artykuł, który właśnie czytasz stanowi jedno z wielu opracowań zagadnień ważnych z punktu widzenia przygotowań do matury z matematyki. Zachęcamy do zajrzenia do zakładki dedykowanej kompleksowym kursom, dzięki którym Twój wynik na maturze będzie jeszcze wyższy!
Źródło: www.freepik.com
1. Rysunek! Pamiętaj – aby o nim, aby lepiej zobrazować sobie zagadnienie opisane w zadaniu. Oczywiście na rysunku będzie niewiele danych i wiele niewiadomych, jednak dysponując poprawnym schematem łatwiej znaleźć zależności pomiędzy jego elementami.
2. Skup się na funkcji, którą optymalizujesz! Przykład: jeżeli w zadaniu masz znaleźć wymiary ostrosłupa prawidłowego czworokątnego, dla którego objętość jest największa (przy pewnych warunkach), twoje skupienie powinno paść na OBJĘTOŚĆ. Do wymiarów dojdziesz, gdy będziesz znał tę największą objętość. Zapisz wzór na objętość, która w przypadku takiego ostrosłupa będzie zależeć od 2 zmiennych: długości podstawy oraz wysokości.
3. Przekształć wzór na optymalizowaną wielość tak, aby był zależny tylko od jednej niewiadomej! Wracając do przykładu, tak jak napisaliśmy, objętość zależy od długości podstawy i wysokości. Twoim zadaniem jest wyeliminowanie z tego równania jednej ze zmiennych! Jak?! Korzystaj z rysunku i treści zadania – na ich podstawie znajdziesz równanie łączące Twoje niewiadome. Wyznacz jedną z nich i wstaw do wzoru funkcji, którą optymalizujesz. W podanym przykładzie takim równaniem może być twierdzenie Pitagorasa wynikające z przekroju ostrosłupa. Na koniec tego kroku powinieneś mieć funkcję zależną od jednej niewiadomej!
4. Pamiętaj o dziedzinie! Na tym etapie zastanów się, jaką dziedzinę ma Twoja funkcja
z podpunktu 3! Nie zapominaj, że dziedzina ograniczona jest również przez rysunek. Przykład: długości nie mogą być ujemne, przeciwprostokątna musi być najdłuższym bokiem w trójkącie.
5. Wyznacz pochodną funkcji z podpunktu 3. oraz znajdź jej ekstrema! Na tym etapie może okazać się (i tak się często dzieje), że Twoja funkcja będzie miała postać iloczynu lub ilorazu, więc pamiętaj o tych wzorach:
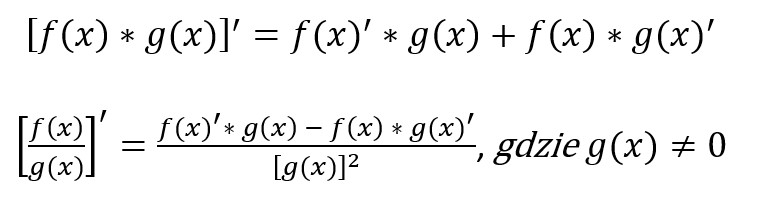
Pamiętaj również, że wyliczone EKSTREMA muszą znajdować się w dziedzinie.
6. Mając już zoptymalizowaną wielkość (wyznaczone ekstrema) wylicz dla niego pozostałe wartości. Przykład: gdy znajdziesz największa objętość, wylicz wymiary ostrosłupa.
UWAGA! W przypadku matury podstawowej również czasem zdarzają się zadania optymalizujące! Jak to?! W zadaniach optymalizacyjnych dla zakresu podstawowego optymalizowana funkcja ma postać FUNKCJI KWADRATOWEJ! Oznacza to, że wartość największą/najmniejszą przyjmuje dla wierzchołka i nie jest wtedy wymagana znajomość pochodnych w celu znalezienia optymalnej wielkości.
To już koniec naszego artykułu, którego tematem była optymalizacja na maturze z matematyki. Zachęcamy do zajrzenia do zakładki dedykowanej przygotowaniom właśnie do matury z tego przedmiotu!
Autor tekstu: Adam Staniucha
Strona przygotowana przez Zyskowni.pl
Zakładamy Ci konto na naszej platformie e-learningowej, na której znajdują się materiały, artykuły popularnonaukowe, czy nagrania video! Możesz tam bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane do sprawdzenia prace.
Na platformie otrzymujesz moduły - zestawy materiałów z prezentacjami, skryptami, testami, kartkówkami. Z nimi pracujesz w dowolnym miejscu - w domu, w podróży, w bibliotece.
Na platformie, gdzie odbywa się kurs możesz zadawać pytania 24h na dobę 7 dni w tygodniu - Prowadzący są tam po to by zawsze Ci pomóc i rozwiać Twoje wątpliwości.
Twój progres w nauce jest kontrolowany wraz z każdym kolejnym modułem - służą temu wszelkie kartkówki, testy i sprawdziany, które rozwiązane odsyłasz i otrzymujesz szczegółowy klucz.
Celujesz w świetny wynik na egzaminie ósmoklasisty? A może potrzebujesz tylko usystematyzować posiadaną wiedzę? Nieważne - nasz kurs (tempo pracy i materiały oraz pomoc Prowadzącego) jest zawsze dopasowany do aktualnego stanu Twoich umiejętności i oczekiwań.
Na platformie otrzymasz nielimitowany w okresie przygotowań dostęp do nagrań video, na których nasz zespół merytoryczny przeprowadzi Cię przez najbardziej wymagające i najczęściej pojawiające się na arkuszu zagadnienia egzaminacyjne.
Indywidualny kurs e-learningowy
egzamin ósmoklasisty
Wolisz uczyć się we własnym tempie i na własnych zasadach? W takim razie kurs e-learningowy jest stworzony właśnie dla Ciebie!
Nowoczesna forma indywidualnej nauki zdalnej (start: natychmiast lub we wskazanym terminie)
Dostęp do dedykowanej platformy do nauki e-learningowej
Harmonogram przygotowań dostosowany do dostępności ucznia
Przypisany opiekun merytoryczny prowadzący kurs
Komplet materiałów podzielonych na moduły tematyczne, a w każdym z nich: prezentacje, testy, kartkówki, skrypty, karty pracy i zadania egzaminacyjne
Materiały video – do kursu dołączone są nagrania video, na których członkowie zespołu merytorycznego IWK tłumaczą najtrudniejsze lub najbardziej prawdopodobne w wystąpieniu na egzaminie zagadnienia
Indywidualne podejście – otrzymujesz dostęp do naszej dedykowanej platformy edukacyjnej z pomocami naukowymi, na której możesz bez ograniczeń kontaktować się ze swoim Opiekunem. Odpowiada on na Twoje pytania i sprawdza wysyłane prace.
Regularnie sprawdzane postępy
Ciągła możliwość kontaktu z Prowadzącym
Dzięki nowoczesnej formie nauki nasze kursy są dostępne dla uczniów z całej Polski – możesz dołączyć do nich niezależnie od miejsca zamieszkania i zacząć przygotowania już dziś! Skontaktuj się z nami i nie odkładaj decyzji na później – do egzaminu ósmoklasisty coraz bliżej!
Grupowy kurs całoroczny
egzamin ósmoklasisty
Chcesz solidnie przygotować się do egzaminu ósmoklasisty? Wolisz regularne zajęcia w grupie i stałe wsparcie prowadzącego? Jeśli tak, kurs grupowy będzie idealnym wyborem dla Ciebie!
46 godzin lekcyjnych zajęć (23 spotkania) + prace domowe
Forma stacjonarna (w salach w Warszawie) lub webinarowa (zajęcia online na żywo)
Nagrania z zajęć webinarowych oraz nagrania umożliwiające nadrobienie materiału osobom zapisującym się po rozpoczęciu kursów stacjonarnych
Możliwość wyboru grupy zajęciowej (harmonogram pojawi się w lipcu 2026 r.)
Pomoc pomiędzy zajęciami – ciągła możliwość kontaktu z Prowadzącym przez dedykowaną grupę zajęciową
Materiały z zajęć w formie cyfrowej
Regularne zajęcia pomagają utrzymać systematyczność w nauce i realnie wpływają na lepsze wyniki na egzaminie ósmoklasisty. Co roku wielu naszych uczniów z różnych części Polski osiąga wysokie rezultaty. Zapisz się na zajęcia już dziś i przygotuj się z nami do egzaminu ósmoklasisty!